Augustin-Jean Fresnel

Augustin-Jean Fresnel
Portrait of "Augustin Fresnel" from the frontispiece of his collected works, 1866
Born	(1788-05-10)10 May 1788 Broglie, Normandy, France
Died	14 July 1827(1827-07-14) (aged 39) Ville-d'Avray, Île-de-France, France
Resting place	Père Lachaise Cemetery
Education	École polytechnique (1804–1806) École des Ponts
Known for	Birefringence Diffraction Fresnel–Arago laws Fresnel equations Fresnel integrals Fresnel lens Fresnel number Fresnel rhomb Fresnel zone Huygens–Fresnel principle Phasor representation Polarization Wave optics
Relatives	Fulgence Fresnel (brother) Léonor Mérimée (uncle) Prosper Mérimée (cousin)
Awards	1819: Academy Grand Prix 1824: Légion d'Honneur 1825: ForMemRS 1827 for '24: Rumford Medal
Scientific career
Fields	Physics, engineering
Institutions	Corps des Ponts Athénée (1819–1820) École Polytech (1821–1824)

Augustin-Jean Fresnel^{[Note 1]} (10 May 1788 – 14 July 1827) was a French civil engineer and physicist whose research in optics led to the almost unanimous acceptance of the wave theory of light, excluding any remnant of Newton's corpuscular theory, from the late 1830s ^[3] until the end of the 19th century. He is perhaps better known for inventing the catadioptric (reflective/refractive) Fresnel lens and for pioneering the use of "stepped" lenses to extend the visibility of lighthouses, saving countless lives at sea. The simpler dioptric (purely refractive) stepped lens, first proposed by Count Buffon ^[4] and independently reinvented by Fresnel, is used in screen magnifiers and in condenser lenses for overhead projectors.

By expressing Huygens's principle of secondary waves and Young's principle of interference in quantitative terms, and supposing that simple colors consist of sinusoidal waves, Fresnel gave the first satisfactory explanation of diffraction by straight edges, including the first satisfactory wave-based explanation of rectilinear propagation.^[5] Part of his argument was a proof that the addition of sinusoidal functions of the same frequency but different phases is analogous to the addition of forces with different directions. By further supposing that light waves are purely transverse, Fresnel explained the nature of polarization, the mechanism of chromatic polarization, and the transmission and reflection coefficients at the interface between two transparent isotropic media. Then, by generalizing the direction-speed-polarization relation for calcite, he accounted for the directions and polarizations of the refracted rays in doubly-refractive crystals of the biaxial class (those for which Huygens's secondary wavefronts are not axisymmetric). The period between the first publication of his pure-transverse-wave hypothesis, and the submission of his first correct solution to the biaxial problem, was less than a year.

Later, he coined the terms linear polarization, circular polarization, and elliptical polarization, explained how optical rotation could be understood as a difference in propagation speeds for the two directions of circular polarization, and (by allowing the reflection coefficient to be complex) accounted for the change in polarization due to total internal reflection, as exploited in the Fresnel rhomb. Defenders of the established corpuscular theory could not match his quantitative explanations of so many phenomena on so few assumptions.

Fresnel had a lifelong battle with tuberculosis, to which he succumbed at the age of 39. Although he did not become a public celebrity in his lifetime, he lived just long enough to receive due recognition from his peers, including (on his deathbed) the Rumford Medal of the Royal Society of London, and his name is ubiquitous in the modern terminology of optics and waves. After the wave theory of light was subsumed by Maxwell's electromagnetic theory in the 1860s, some attention was diverted from the magnitude of Fresnel's contribution. In the period between Fresnel's unification of physical optics and Maxwell's wider unification, a contemporary authority, Humphrey Lloyd, described Fresnel's transverse-wave theory as "the noblest fabric which has ever adorned the domain of physical science, Newton's system of the universe alone excepted." ^[6]

Augustin-Jean Fresnel (also called Augustin Jean or simply Augustin), born in Broglie, Normandy, on 10 May 1788, was the second of four sons of the architect Jacques Fresnel^[11] and his wife Augustine, née Mérimée.^[12] The family moved twice—in 1789/90 to Cherbourg,^[13] and in 1794 ^[14] to Jacques's home town of Mathieu, where Augustine would spend 25 years as a widow,^[15] outliving two of her sons.

The first son, Louis, was admitted to the École Polytechnique, became a lieutenant in the artillery, and was killed in action at Jaca, Spain.^[12] The third, Léonor,^[11] followed Augustin into civil engineering, succeeded him as secretary of the Lighthouse Commission,^[16] and helped to edit his collected works.^[17] The fourth, Fulgence Fresnel, became a linguist, diplomat, and orientalist, and occasionally assisted Augustin with negotiations.^[18][19] Fulgence died in Bagdad in 1855 having led a mission to explore Babylon.^[19]

Madame Fresnel's younger brother, Jean François "Léonor" Mérimée,^[12] father of the writer Prosper Mérimée, was a painter who turned his attention to the chemistry of painting. He became the Permanent Secretary of the École des Beaux-Arts and (until 1814) a professor at the École Polytechnique,^[20] and was the initial point of contact between Augustin and the leading optical physicists of the day (see below).

The Fresnel brothers were initially home-schooled by their mother. The sickly Augustin was considered the slow one, not inclined to memorization;^[21] but the popular story that he hardly began to read until the age of eight is disputed.^[22] At the age of nine or ten he was undistinguished except for his ability to turn tree-branches into toy bows and guns that worked far too well, earning himself the title l'homme de génie (the man of genius) from his accomplices, and a united crackdown from their elders.^[23]

In 1801, Augustin was sent to the École Centrale at Caen, as company for Louis. But Augustin lifted his performance: in late 1804 he was accepted into the École Polytechnique, being placed 17th in the entrance examination.^[24][25] As the detailed records of the École Polytechnique begin in 1808, we know little of Augustin's time there, except that he made few if any friends and—in spite of continuing poor health—excelled in drawing and geometry:^[26] in his first year he took a prize for his solution to a geometry problem posed by Adrien-Marie Legendre.^[27] Graduating in 1806, he then enrolled at the École Nationale des Ponts et Chaussées (National School of Bridges and Roads, also known as "ENPC" or "École des Ponts"), from which he graduated in 1809, entering the service of the Corps des Ponts et Chaussées as an ingénieur ordinaire aspirant (ordinary engineer in training). Directly or indirectly, he was to remain in the employment of the "Corps des Ponts" for the rest of his life.^[28]

Fresnel's parents were Roman Catholics of the Jansenist sect, characterized by an extreme Augustinian view of original sin. Religion took first place in the boys' home-schooling. In 1802, his mother said:

I pray God to give my son the grace to employ the great talents, which he has received, for his own benefit, and for the God of all. Much will be asked from him to whom much has been given, and most will be required of him who has received most.^[29]

Augustin remained a Jansenist.^[30] He regarded his intellectual talents as gifts from God, and considered it his duty to use them for the benefit of others.^[31] According to his fellow engineer Alphonse Duleau, who helped to nurse him through his final illness, Fresnel saw the study of nature as part of the study of the power and goodness of God. He placed virtue above science and genius. In his last days he prayed for "strength of soul," not against death alone, but against "the interruption of discoveries… of which he hoped to derive useful applications." ^[32]

Jansenism is considered heretical by the Roman Catholic Church, and Grattan-Guinness suggests this is why Fresnel never gained a permanent academic teaching post;^[33] his only teaching appointment was at the Athénée in the winter of 1819–20.^[34][35] The article on Fresnel in the Catholic Encyclopedia does not mention his Jansenism, but describes him as "a deeply religious man and remarkable for his keen sense of duty." ^[34]

Fresnel was initially posted to the western département of Vendée. There, in 1811, he anticipated what became known as the Solvay process for producing soda ash, except that recycling of the ammonia was not considered.^[36] That difference may explain why leading chemists, who learned of his discovery through his uncle Léonor, eventually thought it uneconomic.^[37]

About 1812, Fresnel was sent to Nyons, in the southern département of Drôme, to assist with the imperial highway that was to connect Spain and Italy.^[14] It is from Nyons that we have the first evidence of his interest in optics. On 15 May 1814, while work was slack due to Napoleon's defeat,^[38] Fresnel wrote a "P.S." to his brother Léonor, saying in part:

I would also like to have papers that might tell me about the discoveries of French physicists on the polarization of light. I saw in the Moniteur of a few months ago that Biot had read to the Institute a very interesting memoir on the polarization of light. Though I break my head, I cannot guess what that is.^[39]

As late as 28 December he was still waiting for information, but by 10 February 1815 he had received Biot's memoir.^[40] (The Institut de France had taken over the functions of the French Académie des Sciences and other académies in 1795. In 1816 the Académie des Sciences regained its name and autonomy, but remained part of the institute.^[41])

In March 1815, perceiving Napoleon's return from Elba as "an attack on civilization",^[42] Fresnel departed without leave, hastened to Toulouse and offered his services to the royalist resistance, but soon found himself on the sick list. Returning to Nyons in defeat, he was threatened and had his windows broken. During the Hundred Days he was placed on suspension, which he was eventually allowed to spend at his mother's house in Mathieu. There he used his enforced leisure to begin his optical experiments.^[43]

The appreciation of Fresnel's reconstruction of physical optics might be assisted by an overview of the fragmented state in which he found the subject. In this subsection, optical phenomena that were unexplained or whose explanations were disputed are named in bold type.

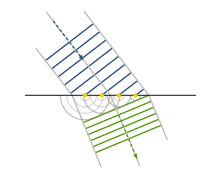
The corpuscular theory of light, favored by Isaac Newton and accepted by nearly all of Fresnel's seniors, easily explained rectilinear propagation: the corpuscles obviously moved very fast, so that their paths were very nearly straight. The wave theory, as developed by Christiaan Huygens in his Treatise on Light (1690), explained rectilinear propagation on the assumption that each point crossed by a traveling wavefront becomes the source of a secondary wavefront. Given the initial position of a traveling wavefront, any later position (according to Huygens) was the common tangent surface (envelope) of the secondary wavefronts emitted from the earlier position.^[44] As the extent of the common tangent was limited by the extent of the initial wavefront, the repeated application of Huygens's construction to a plane wavefront of limited extent (in a uniform medium) gave a straight, parallel beam. While this construction indeed predicted rectilinear propagation, it was difficult to reconcile with the common observation that wavefronts on the surface of water can bend around obstructions, and with the similar behavior of sound waves—causing Newton to maintain, to the end of his life, that if light consisted of waves it would "bend and spread every way" into the shadows.^[45]

Huygens's theory neatly explained the law of ordinary reflection and the law of ordinary refraction ("Snell's law"), provided that the secondary waves traveled slower in denser media (those of higher refractive index).^[46] The corpuscular theory, with the hypothesis that the corpuscles were subject to forces acting perpendicular to surfaces, explained the same laws equally well,^[47] albeit with the implication that light traveled faster in denser media; that implication was wrong, but could not be directly disproven with the technology of Newton's time or even Fresnel's time (see Foucault's measurements of the speed of light).

Similarly inconclusive was stellar aberration—that is, the apparent change in the position of a star due to the velocity of the earth across the line of sight (not to be confused with stellar parallax, which is due to the displacement of the earth across the line of sight). Identified by James Bradley in 1728, stellar aberration was widely taken as confirmation of the corpuscular theory. But it was equally compatible with the wave theory, as Euler noted in 1746—tacitly assuming that the aether (the supposed wave-bearing medium) near the earth was not disturbed by the motion of the earth.^[48]

The outstanding strength of Huygens's theory was his explanation of the birefringence (double refraction) of "Iceland crystal" (transparent calcite), on the assumption that the secondary waves are spherical for the ordinary refraction (which satisfies Snell's law) and spheroidal for the extraordinary refraction (which does not).^[49] In general, Huygens's common-tangent construction implies that rays are paths of least time between successive positions of the wavefront, in accordance with Fermat's principle.^[50][51] In the special case of isotropic media, the secondary wavefronts must be spherical, and Huygens's construction then implies that the rays are perpendicular to the wavefront; indeed, the law of ordinary refraction can be separately derived from that premise, as Ignace-Gaston Pardies did before Huygens.^[52]

Although Newton rejected the wave theory, he noticed its potential to explain colors, including the colors of "thin plates" (e.g., "Newton's rings", and the colors of skylight reflected in soap bubbles), on the assumption that light consists of periodic waves, with the lowest frequencies (longest wavelengths) at the red end of the spectrum, and the highest frequencies (shortest wavelengths) at the violet end. In 1672 he published a heavy hint to that effect,^{[53][54]: 5088–5089} but contemporary supporters of the wave theory failed to act on it: Robert Hooke treated light as a periodic sequence of pulses but did not use frequency as the criterion of color,^[55] while Huygens treated the waves as individual pulses without any periodicity;^[56] and Pardies died young in 1673. Newton himself tried to explain colors of thin plates using the corpuscular theory, by supposing that his corpuscles had the wavelike property of alternating between "fits of easy transmission" and "fits of easy reflection",^[57] the distance between like "fits" depending on the color and the medium ^[58] and, awkwardly, on the angle of refraction or reflection into that medium.^{[59][60]: 1144} More awkwardly still, this theory required thin plates to reflect only at the back surface, although thick plates manifestly reflected also at the front surface.^[61] It was not until 1801 that Thomas Young, in the Bakerian Lecture for that year, cited Newton's hint,^{[62]: 18–19} and accounted for the colors of a thin plate as the combined effect of the front and back reflections, which reinforce or cancel each other according to the wavelength and the thickness.^{[62]: 37–39} Young similarly explained the colors of "striated surfaces" (e.g., gratings) as the wavelength-dependent reinforcement or cancellation of reflections from adjacent lines.^{[62]: 35–37} He described this reinforcement or cancellation as interference.

Neither Newton nor Huygens satisfactorily explained diffraction—the blurring and fringing of shadows where, according to rectilinear propagation, they ought to be sharp. Newton, who called diffraction "inflexion", supposed that rays of light passing close to obstacles were bent ("inflected"); but his explanation was only qualitative.^[63] Huygens's common-tangent construction, without modifications, could not accommodate diffraction at all. Two such modifications were proposed by Young in the same 1801 Bakerian Lecture: first, that the secondary waves near the edge of an obstacle could diverge into the shadow, but only weakly, due to limited reinforcement from other secondary waves;^{[62]: 25–27} and second, that diffraction by an edge was caused by interference between two rays: one reflected off the edge, and the other inflected while passing near the edge. The latter ray would be undeviated if sufficiently far from the edge, but Young did not elaborate on that case.^{[62]: 42–44} These were the earliest suggestions that the degree of diffraction depends on wavelength.^[64] Later, in the 1803 Bakerian Lecture, Young ceased to regard inflection as a separate phenomenon,^[65] and produced evidence that diffraction fringes inside the shadow of a narrow obstacle were due to interference: when the light from one side was blocked, the internal fringes disappeared.^[66] But Young was alone in such efforts until Fresnel entered the field.^[67]

Huygens, in his investigation of double refraction, noticed something that he could not explain: when light passes through two similarly oriented calcite crystals at normal incidence, the ordinary ray emerging from the first crystal suffers only the ordinary refraction in the second, while the extraordinary ray emerging from the first suffers only the extraordinary refraction in the second; but when the second crystal is rotated 90° about the incident rays, the roles are interchanged, so that the ordinary ray emerging from the first crystal suffers only the extraordinary refraction in the second, and vice versa.^[68] This discovery gave Newton another reason to reject the wave theory: rays of light evidently had "sides".^[69] Corpuscles could have sides ^[70] (or poles, as they would later be called); but waves of light could not,^[71] because (so it seemed) any such waves would need to be longitudinal (with vibrations in the direction of propagation). Newton offered an alternative "Rule" for the extraordinary refraction,^[72] which rode on his authority through the 18th century, although he made "no known attempt to deduce it from any principles of optics, corpuscular or otherwise." ^[73]: 327

In 1808, the extraordinary refraction of calcite was investigated experimentally, with unprecedented accuracy, by Étienne-Louis Malus, and found to be consistent with Huygens's spheroid construction, not Newton's "Rule".^[73] Malus, encouraged by Pierre-Simon Laplace,^[60]: 1146 then sought to explain this law in corpuscular terms: from the known relation between the incident and refracted ray directions, Malus derived the corpuscular velocity (as a function of direction) that would satisfy Maupertuis's "least action" principle. But, as Young pointed out, the existence of such a velocity law was guaranteed by Huygens's spheroid, because Huygens's construction leads to Fermat's principle, which becomes Maupertuis's principle if the ray speed is replaced by the reciprocal of the particle speed! The corpuscularists had not found a force law that would yield the alleged velocity law, except by a circular argument in which a force acting at the surface of the crystal inexplicably depended on the direction of the (possibly subsequent) velocity within the crystal. Worse, it was doubtful that any such force would satisfy the conditions of Maupertuis's principle.^[74] In contrast, Young proceeded to show that "a medium more easily compressible in one direction than in any direction perpendicular to it, as if it consisted of an infinite number of parallel plates connected by a substance somewhat less elastic" admits spheroidal longitudinal wavefronts, as Huygens supposed.^[75]

But Malus, in the midst of his experiments on double refraction, noticed something else: when a ray of light is reflected off a non-metallic surface at the appropriate angle, it behaves like one of the two rays emerging from a calcite crystal.^[76] It was Malus who coined the term polarization to describe this behavior, although the polarizing angle became known as Brewster's angle after its dependence on the refractive index was determined experimentally by David Brewster in 1815.^[77] Malus also introduced the term plane of polarization. In the case of polarization by reflection, his "plane of polarization" was the plane of the incident and reflected rays; in modern terms, this is the plane normal to the electric vibration. In 1809, Malus further discovered that the intensity of light passing through two polarizers is proportional to the squared cosine of the angle between their planes of polarization (Malus's law),^[78] whether the polarizers work by reflection or double refraction, and that all birefringent crystals produce both extraordinary refraction and polarization.^[79] As the corpuscularists started trying to explain these things in terms of polar "molecules" of light, the wave-theorists had no working hypothesis on the nature of polarization, prompting Young to remark that Malus's observations "present greater difficulties to the advocates of the undulatory theory than any other facts with which we are acquainted." ^[80]

Malus died in February 1812, at the age of 36, shortly after receiving the Rumford Medal for his work on polarization.

In August 1811, François Arago reported that if a thin plate of mica was viewed against a white polarized backlight through a calcite crystal, the two images of the mica were of complementary colors (the overlap having the same color as the background). The light emerging from the mica was "depolarized" in the sense that there was no orientation of the calcite that made one image disappear; yet it was not ordinary ("unpolarized") light, for which the two images would be of the same color. Rotating the calcite around the line of sight changed the colors, though they remained complementary. Rotating the mica changed the saturation (not the hue) of the colors. This phenomenon became known as chromatic polarization. Replacing the mica with a much thicker plate of quartz, with its faces perpendicular to the optic axis (the axis of Huygens's spheroid or Malus's velocity function), produced a similar effect, except that rotating the quartz made no difference. Arago tried to explain his observations in corpuscular terms.^[81]

In 1812, as Arago pursued further qualitative experiments and other commitments, Jean-Baptiste Biot reworked the same ground using a gypsum lamina in place of the mica, and found empirical formulae for the intensities of the ordinary and extraordinary images. The formulae contained two coefficients, supposedly representing colors of rays "affected" and "unaffected" by the plate—the "affected" rays being of the same color mix as those reflected by amorphous thin plates of proportional, but lesser, thickness.^[82]

Arago protested, declaring that he had made some of the same discoveries but had not had time to write them up. In fact the overlap between Arago's work and Biot's was minimal, Arago's being only qualitative and wider in scope (attempting to include polarization by reflection). But the dispute triggered a notorious falling-out between the two men.^[83][84]

Later that year, Biot tried to explain the observations as an oscillation of the alignment of the "affected" corpuscles at a frequency proportional to that of Newton's "fits", due to forces depending on the alignment. This theory became known as mobile polarization. To reconcile his results with a sinusoidal oscillation, Biot had to suppose that the corpuscles emerged with one of two permitted orientations, namely the extremes of the oscillation, with probabilities depending on the phase of the oscillation.^[85] Corpuscular optics was becoming expensive on assumptions. But in 1813, Biot reported that the case of quartz was simpler: the observable phenomenon (now called optical rotation or optical activity or sometimes rotary polarization) was a gradual rotation of the polarization direction with distance, and could be explained by a corresponding rotation (not oscillation) of the corpuscles.^[86]

Early in 1814, reviewing Biot's work on chromatic polarization, Young noted that the periodicity of the color as a function of the plate thickness—including the factor by which the period exceeded that for a reflective thin plate, and even the effect of obliquity of the plate (but not the role of polarization)—could be explained by the wave theory in terms of the different propagation times of the ordinary and extraordinary waves through the plate.^[87] But Young was then the only public defender of the wave theory.^[88]

In summary, in the spring of 1814, as Fresnel tried in vain to guess what polarization was, the corpuscularists thought that they knew, while the wave-theorists (if we may use the plural) literally had no idea. Both theories claimed to explain rectilinear propagation, but the wave explanation was overwhelmingly regarded as unconvincing. The corpuscular theory could not rigorously link double refraction to surface forces; the wave theory could not yet link it to polarization. The corpuscular theory was weak on thin plates and silent on gratings;^{[Note 2]} the wave theory was strong on both, but under-appreciated. Concerning diffraction, the corpuscular theory did not yield quantitative predictions, while the wave theory had begun to do so by considering diffraction as a manifestation of interference, but had only considered two rays at a time. Only the corpuscular theory gave even a vague insight into Brewster's angle, Malus's law, or optical rotation. Concerning chromatic polarization, the wave theory explained the periodicity far better than the corpuscular theory, but had nothing to say about the role of polarization; and its explanation of the periodicity was largely ignored.^[89] And Arago had founded the study of chromatic polarization, only to lose the lead, controversially, to Biot. Such were the circumstances in which Arago first heard of Fresnel's interest in optics.

Fresnel's letters from later in 1814 reveal his interest in the wave theory, including his awareness that it explained the constancy of the speed of light and was at least compatible with stellar aberration. Eventually he compiled what he called his rêveries (musings) into an essay and submitted it via Léonor Mérimée to André-Marie Ampère, who did not respond directly. But on 19 December, Mérimée dined with Ampère and Arago, with whom he was acquainted through the École Polytechnique; and Arago promised to look at Fresnel's essay.^{[90][Note 3]}

In mid 1815, on his way home to Mathieu to serve his suspension, Fresnel met Arago in Paris and spoke of the wave theory and stellar aberration. He was informed that he was trying to break down open doors ("il enfonçait des portes ouvertes"), and directed to classical works on optics.^[91]

On 12 July 1815, as Fresnel was about to leave Paris, Arago left him a note on a new topic:

I do not know of any book that contains all the experiments that physicists are doing on the diffraction of light. M'sieur Fresnel will only be able to get to know this part of the optics by reading the work by Grimaldi, the one by Newton, the English treatise by Jordan,^[92] and the memoirs of Brougham and Young, which are part of the collection of the Philosophical Transactions.^[93]

Fresnel would not have ready access to these works outside Paris, and could not read English.^[94] But, in Mathieu—with a point-source of light made by focusing sunlight with a drop of honey, a crude micrometer of his own construction, and supporting apparatus made by a local locksmith—he began his own experiments.^[95] His technique was novel: whereas earlier investigators had projected the fringes onto a screen, Fresnel soon abandoned the screen and observed the fringes in space, through a lens with the micrometer at its focus, allowing more accurate measurements while requiring less light.^[96]

Later in July, after Napoleon's final defeat, Fresnel was reinstated with the advantage of having backed the winning side. He requested a two-month leave of absence, which was readily granted because roadworks were in abeyance.^[97]

On 23 September he wrote to Arago, beginning "I think I have found the explanation and the law of colored fringes which one notices in the shadows of bodies illuminated by a luminous point." In the same paragraph, however, Fresnel implicitly acknowledged doubt about the novelty of his work: noting that he would need to incur some expense in order to improve his measurements, he wanted to know "whether this is not useless, and whether the law of diffraction has not already been established by sufficiently exact experiments." ^[98] He explained that he had not yet had a chance to acquire the items on his reading lists,^[94] with the apparent exception of "Young's book", which he could not understand without his brother's help.^{[99][Note 4]}  Not surprisingly, he had retraced many of Young's steps.

In a memoir sent to the institute on 15 October 1815, Fresnel mapped the external and internal fringes in the shadow of a wire. He noticed, like Young before him, that the internal fringes disappeared when the light from one side was blocked, and concluded that "the vibrations of two rays that cross each other under a very small angle can contradict each other…" ^[100] But, whereas Young took the disappearance of the internal fringes as confirmation of the principle of interference, Fresnel reported that it was the internal fringes that first drew his attention to the principle. To explain the diffraction pattern, Fresnel constructed the internal fringes by considering the intersections of circular wavefronts emitted from the two edges of the obstruction, and the external fringes by considering the intersections between direct waves and waves reflected off the nearer edge. For the external fringes, to obtain tolerable agreement with observation, he had to suppose that the reflected wave was inverted; and he noted that the predicted paths of the fringes were hyperbolic. In the part of the memoir that most clearly surpassed Young, Fresnel explained the ordinary laws of reflection and refraction in terms of interference, noting that if two parallel rays were reflected or refracted at other than the prescribed angle, they would no longer have the same phase in a common perpendicular plane, and every vibration would be cancelled by a nearby vibration. He noted that his explanation was valid provided that the surface irregularities were much smaller than the wavelength.^[101]

On 10 November, Fresnel sent a supplementary note dealing with Newton's rings and with gratings,^[102] including, for the first time, transmission gratings—although in that case the interfering rays were still assumed to be "inflected", and the experimental verification was inadequate because it used only two threads.^[103]

As Fresnel was not a member of the institute, the fate of his memoir depended heavily on the report of a single member. The reporter for Fresnel's memoir turned out to be Arago (with Poinsot as the other reviewer).^[104] On 8 November, Arago wrote to Fresnel:

I have been instructed by the Institute to examine your memoir on the diffraction of light; I have studied it carefully, and found many interesting experiments, some of which had already been done by Dr. Thomas Young, who in general regards this phenomenon in a manner rather analogous to the one you have adopted. But what neither he nor anyone had seen before you is that the external colored bands do not travel in a straight line as one moves away from the opaque body. The results you have achieved in this regard seem to me very important; perhaps they can serve to prove the truth of the undulatory system, so often and so feebly combated by physicists who have not bothered to understand it.^[105]

Fresnel was troubled, wanting to know more precisely where he had collided with Young.^[106] Concerning the curved paths of the "colored bands", Young had noted the hyperbolic paths of the fringes in the two-source interference pattern, corresponding roughly to Fresnel's internal fringes, and had described the hyperbolic fringes that appear on the screen within rectangular shadows.^[107] He had not mentioned the curved paths of the external fringes of a shadow; but, as he later explained,^[108] that was because Newton had already done so.^[109] Newton evidently thought the fringes were caustics. Thus Arago erred in his belief that the curved paths of the fringes were fundamentally incompatible with the corpuscular theory.^[110]

Arago's letter went on to request more data on the external fringes. Fresnel complied, until he exhausted his leave and was assigned to Rennes in the département of Ille-et-Vilaine. At this point Arago interceded with Gaspard de Prony, head of the École des Ponts, who wrote to Louis-Mathieu Molé, head of the Corps des Ponts, suggesting that the progress of science and the prestige of the Corps would be enhanced if Fresnel could come to Paris for a time. He arrived in March 1816, and his leave was subsequently extended through the middle of the year.^[111]

Meanwhile, in an experiment reported on 26 February 1816, Arago verified Fresnel's prediction that the internal fringes were shifted if the rays on one side of the obstacle passed through a thin glass lamina. Fresnel correctly attributed this phenomenon to the lower wave velocity in the glass.^[112] Arago later used a similar argument to explain the colors in the scintillation of stars.^{[Note 5]}

Fresnel's updated memoir ^[113] was eventually published in the March 1816 issue of Annales de Chimie et de Physique, of which Arago had recently become co-editor.^[114] That issue did not actually appear until May.^[115] In March, Fresnel already had competition: Biot read a memoir on diffraction by himself and his student Claude Pouillet, containing copious data and arguing that the regularity of diffraction fringes, like the regularity of Newton's rings, must be linked to Newton's "fits". But the new link was not rigorous, and Pouillet himself would become a distinguished early adopter of the wave theory.^[116]

On 24 May 1816, Fresnel wrote to Young (in French), acknowledging how little of his own memoir was new.^[118] But in a "supplement" signed on 14 July and read the next day,^[119] Fresnel noted that the internal fringes were more accurately predicted by supposing that the two interfering rays came from some distance outside the edges of the obstacle. To explain this, he divided the incident wavefront at the obstacle into what we now call Fresnel zones, such that the secondary waves from each zone were spread over half a cycle when they arrived at the observation point. The zones on one side of the obstacle largely canceled out in pairs, except the first zone, which was represented by an "efficacious ray". This approach worked for the internal fringes, but the superposition of the efficacious ray and the direct ray did not work for the external fringes.^[120]

The contribution from the "efficacious ray" was thought to be only partly canceled, for reasons involving the dynamics of the medium: where the wavefront was continuous, symmetry forbade oblique vibrations; but near the obstacle that truncated the wavefront, the asymmetry allowed some sideways vibration towards the geometric shadow. This argument showed that Fresnel had not (yet) fully accepted Huygens's principle, which would have permitted oblique radiation from all portions of the front.^[121]

In the same supplement, Fresnel described his well-known double mirror, comprising two flat mirrors joined at an angle of slightly less than 180°, with which he produced a two-slit interference pattern from two virtual images of the same slit. A conventional double-slit experiment required a preliminary single slit to ensure that the light falling on the double slit was coherent (synchronized). In Fresnel's version, the preliminary single slit was retained, and the double slit was replaced by the double mirror—which bore no physical resemblance to the double slit and yet performed the same function. This result (which had been announced by Arago in the March issue of the Annales) made it hard to believe that the two-slit pattern had anything to do with corpuscles being deflected as they passed near the edges of the slits.^[122]

But 1816 was the "Year Without a Summer": crops failed; hungry farming families lined the streets of Rennes; the central government organized "charity workhouses" for the needy; and in October, Fresnel was sent back to Ille-et-Vilaine to supervise charity workers in addition to his regular road crew.^[123] According to Arago,

with Fresnel conscientiousness was always the foremost part of his character, and he constantly performed his duties as an engineer with the most rigorous scrupulousness. The mission to defend the revenues of the state, to obtain for them the best employment possible, appeared to his eyes in the light of a question of honour. The functionary, whatever might be his rank, who submitted to him an ambiguous account, became at once the object of his profound contempt. … Under such circumstances the habitual gentleness of his manners disappeared…^[124]

Fresnel's letters from December 1816 reveal his consequent anxiety. To Arago he complained of being "tormented by the worries of surveillance, and the need to reprimand…" And to Mérimée he wrote: "I find nothing more tiresome than having to manage other men, and I admit that I have no idea what I'm doing." ^[125]

On 17 March 1817, the Académie des Sciences announced that diffraction would be the topic for the biannual physics Grand Prix to be awarded in 1819.^[126] The deadline for entries was set at 1 August 1818 to allow time for replication of experiments. Although the wording of the problem referred to rays and inflection and did not invite wave-based solutions, Arago and Ampère encouraged Fresnel to enter.^[127]

In the fall of 1817, Fresnel, supported by de Prony, obtained a leave of absence from the new head of the Corp des Ponts, Louis Becquey, and returned to Paris.^[128] He resumed his engineering duties in the spring of 1818; but from then on he was based in Paris,^[129] first on the Canal de l'Ourcq,^[130] and then (from May 1819) with the cadastre of the pavements.^{[131][132]: 486}

On 15 January 1818, in a different context (revisited below), Fresnel showed that the addition of sinusoidal functions of the same frequency but different phases is analogous to the addition of forces with different directions.^[133] His method was similar to the phasor representation, except that the "forces" were plane vectors rather than complex numbers; they could be added, and multiplied by scalars, but not (yet) multiplied and divided by each other. The explanation was algebraic rather than geometric.

Knowledge of this method was assumed in a preliminary note on diffraction,^[134] dated 19 April 1818 and deposited on 20 April, in which Fresnel outlined the elementary theory of diffraction as found in modern textbooks. He restated Huygens's principle in combination with the superposition principle, saying that the vibration at each point on a wavefront is the sum of the vibrations that would be sent to it at that moment by all the elements of the wavefront in any of its previous positions, all elements acting separately (see Huygens–Fresnel principle). For a wavefront partly obstructed in a previous position, the summation was to be carried out over the unobstructed portion. In directions other than the normal to the primary wavefront, the secondary waves were weakened due to obliquity, but weakened much more by destructive interference, so that the effect of obliquity alone could be ignored.^[135] For diffraction by a straight edge, the intensity as a function of distance from the geometric shadow could then be expressed with sufficient accuracy in terms of what are now called the normalized Fresnel integrals:

${\displaystyle C(x)=\!\int _{0}^{x}\!\cos {\big (}{\tfrac {1}{2}}\pi z^{2}{\big )}\,dz}$    ${\displaystyle S(x)=\!\int _{0}^{x}\!\sin {\big (}{\tfrac {1}{2}}\pi z^{2}{\big )}\,dz\,.}$

The same note included a table of the integrals, for an upper limit ranging from 0 to 5.1 in steps of 0.1, computed with a mean error of 0.0003,^[136] plus a smaller table of maxima and minima of the resulting intensity.

In his final "Memoir on the diffraction of light",^[137] deposited on 29 July ^[138] and bearing the Latin epigraph "Natura simplex et fecunda" ("Nature simple and fertile"),^[139] Fresnel slightly expanded the two tables without changing the existing figures, except for a correction to the first minimum of intensity. For completeness, he repeated his solution to "the problem of interference", whereby sinusoidal functions are added like vectors. He acknowledged the directionality of the secondary sources and the variation in their distances from the observation point, chiefly to explain why these things make negligible difference in the context, provided of course that the secondary sources do not radiate in the retrograde direction. Then, applying his theory of interference to the secondary waves, he expressed the intensity of light diffracted by a single straight edge (half-plane) in terms of integrals which involved the dimensions of the problem, but which could be converted to the normalized forms above. With reference to the integrals, he explained the calculation of the maxima and minima of the intensity (external fringes), and noted that the calculated intensity falls very rapidly as one moves into the geometric shadow.^[140] The last result, as Olivier Darrigol says, "amounts to a proof of the rectilinear propagation of light in the wave theory, indeed the first proof that a modern physicist would still accept." ^[141]

For the experimental testing of his calculations, Fresnel used red light with a wavelength of 638 nm, which he deduced from the diffraction pattern in the simple case in which light incident on a single slit was focused by a cylindrical lens. For a variety of distances from the source to the obstacle and from the obstacle to the field point, he compared the calculated and observed positions of the fringes for diffraction by a half-plane, a slit, and a narrow strip—concentrating on the minima, which were visually sharper than the maxima. For the slit and the strip, he could not use the previously computed table of maxima and minima; for each combination of dimensions, the intensity had to be expressed in terms of sums or differences of Fresnel integrals and calculated from the table of integrals, and the extrema had to be calculated anew.^[142] The agreement between calculation and measurement was better than 1.5% in almost every case.^[143]

Near the end of the memoir, Fresnel summed up the difference between Huygens's use of secondary waves and his own: whereas Huygens says there is light only where the secondary waves exactly agree, Fresnel says there is complete darkness only where the secondary waves exactly cancel out.^[144]

The judging committee comprised Laplace, Biot, and Poisson (all corpuscularists), Gay-Lussac (uncommitted), and Arago, who eventually wrote the committee's report.^[145] Although entries in the competition were supposed to be anonymous to the judges, Fresnel's must have been recognizable by the content.^[146] There was only one other entry, of which neither the manuscript nor any record of the author has survived.^[147] That entry (identified as "no. 1") was mentioned only in the last paragraph of the judges' report,^[148] noting that the author had shown ignorance of the relevant earlier works of Young and Fresnel, used insufficiently precise methods of observation, overlooked known phenomena, and made obvious errors. In the words of John Worrall, "The competition facing Fresnel could hardly have been less stiff." ^[149] We may infer that the committee had only two options: award the prize to Fresnel ("no. 2"), or withhold it.^[150]

The committee deliberated into the new year.^[151]: 144 Then Poisson, exploiting a case in which Fresnel's theory gave easy integrals, predicted that if a circular obstacle were illuminated by a point-source, there should be (according to the theory) a bright spot in the center of the shadow, illuminated as brightly as the exterior. This seems to have been intended as a reductio ad absurdum. Arago, undeterred, assembled an experiment with an obstacle 2 mm in diameter—and there, in the center of the shadow, was Poisson's spot.^[152]

The unanimous ^[153] report of the committee,^[154] read at the meeting of the Académie on 15 March 1819,^[155] awarded the prize to "the memoir marked no. 2, and bearing as epigraph: Natura simplex et fecunda." ^[156] At the same meeting,^[157]: 427 after the judgment was delivered, the president of the Académie opened a sealed note accompanying the memoir, revealing the author as Fresnel.^[158] The award was announced at the public meeting of the Académie a week later, on 22 March.^[157]: 432

Arago's verification of Poisson's counter-intuitive prediction passed into folklore as if it had decided the prize.^[159] That view, however, is not supported by the judges' report, which gave the matter only two sentences in the penultimate paragraph.^[160] Neither did Fresnel's triumph immediately convert Laplace, Biot, and Poisson to the wave theory,^[161] for at least four reasons. First, although the professionalization of science in France had established common standards, it was one thing to acknowledge a piece of research as meeting those standards, and another thing to regard it as conclusive.^[88] Second, it was possible to interpret Fresnel's integrals as rules for combining rays. Arago even encouraged that interpretation, presumably in order to minimize resistance to Fresnel's ideas.^[162] Even Biot began teaching the Huygens-Fresnel principle without committing himself to a wave basis.^[163] Third, Fresnel's theory did not adequately explain the mechanism of generation of secondary waves or why they had any significant angular spread; this issue particularly bothered Poisson.^[164] Fourth, the question that most exercised optical physicists at that time was not diffraction, but polarization—on which Fresnel had been working, but was yet to make his critical breakthrough.

An emission theory of light was one that regarded the propagation of light as the transport of some kind of matter. While the corpuscular theory was obviously an emission theory, the converse did not follow: in principle, one could be an emissionist without being a corpuscularist. This was convenient because, beyond the ordinary laws of reflection and refraction, emissionists never managed to make testable quantitative predictions from a theory of forces acting on corpuscles of light. But they did make quantitative predictions from the premises that rays were countable objects, which were conserved in their interactions with matter (except absorbent media), and which had particular orientations with respect to their directions of propagation. According to this framework, polarization and the related phenomena of double refraction and partial reflection involved altering the orientations of the rays and/or selecting them according to orientation, and the state of polarization of a beam (a bundle of rays) was a question of how many rays were in what orientations: in a fully polarized beam, the orientations were all the same. This approach, which Jed Buchwald has called selectionism, was pioneered by Malus and diligently pursued by Biot.^{[165][84]: 110–113}

Fresnel, in contrast, decided to introduce polarization into interference experiments.

In July or August 1816, Fresnel discovered that when a birefringent crystal produced two images of a single slit, he could not obtain the usual two-slit interference pattern, even if he compensated for the different propagation times. A more general experiment, suggested by Arago, found that if the two beams of a double-slit device were separately polarized, the interference pattern appeared and disappeared as the polarization of one beam was rotated, giving full interference for parallel polarizations, but no interference for perpendicular polarizations (see Fresnel–Arago laws).^[166] These experiments, among others, were eventually reported in a brief memoir published in 1819 and later translated into English.^[167]

In a memoir drafted on 30 August 1816 and revised on 6 October, Fresnel reported an experiment in which he placed two matching thin laminae in a double-slit apparatus—one over each slit, with their optic axes perpendicular—and obtained two interference patterns offset in opposite directions, with perpendicular polarizations. This, in combination with the previous findings, meant that each lamina split the incident light into perpendicularly polarized components with different velocities—just like a normal (thick) birefringent crystal, and contrary to Biot's "mobile polarization" hypothesis.^[168]

Accordingly, in the same memoir, Fresnel offered his first attempt at a wave theory of chromatic polarization. When polarized light passed through a crystal lamina, it was split into ordinary and extraordinary waves (with intensities described by Malus's law), and these were perpendicularly polarized and therefore did not interfere, so that no colors were produced (yet). But if they then passed through an analyzer (second polarizer), their polarizations were brought into alignment (with intensities again modified according to Malus's law), and they would interfere.^[169] This explanation, by itself, predicts that if the analyzer is rotated 90°, the ordinary and extraordinary waves simply switch roles, so that if the analyzer takes the form of a calcite crystal, the two images of the lamina should be of the same hue (this issue is revisited below). But in fact, as Arago and Biot had found, they are of complementary colors. To correct the prediction, Fresnel proposed a phase-inversion rule whereby one of the constituent waves of one of the two images suffered an additional 180° phase shift on its way through the lamina. This inversion was a weakness in the theory relative to Biot's, as Fresnel acknowledged,^[170] although the rule specified which of the two images had the inverted wave.^[171] Moreover, Fresnel could deal only with special cases, because he had not yet solved the problem of superposing sinusoidal functions with arbitrary phase differences due to propagation at different velocities through the lamina.^[172]

He solved that problem in a "supplement" signed on 15 January 1818 ^[133] (mentioned above). In the same document, he accommodated Malus's law by proposing an underlying law: that if polarized light is incident on a birefringent crystal with its optic axis at an angle θ to the "plane of polarization", the ordinary and extraordinary vibrations (as functions of time) are scaled by the factors cos θ and sin θ, respectively. Although modern readers easily interpret these factors in terms of perpendicular components of a transverse oscillation, Fresnel did not (yet) explain them that way. Hence he still needed the phase-inversion rule. He applied all these principles to a case of chromatic polarization not covered by Biot's formulae, involving two successive laminae with axes separated by 45°, and obtained predictions that disagreed with Biot's experiments (except in special cases) but agreed with his own.^[173]

Fresnel applied the same principles to the standard case of chromatic polarization, in which one birefringent lamina was sliced parallel to its axis and placed between a polarizer and an analyzer. If the analyzer took the form of a thick calcite crystal with its axis in the plane of polarization, Fresnel predicted that the intensities of the ordinary and extraordinary images of the lamina were respectively proportional to

${\displaystyle I_{o}=\cos ^{2}i\,\cos ^{2}(i{-}s)+\sin ^{2}i\,\sin ^{2}(i{-}s)+{\tfrac {1}{2}}\sin 2i\,\sin 2(i{-}s)\cos \phi \,,}$

${\displaystyle I_{e}=\cos ^{2}i\,\sin ^{2}(i{-}s)+\sin ^{2}i\,\cos ^{2}(i{-}s)-{\tfrac {1}{2}}\sin 2i\,\sin 2(i{-}s)\cos \phi \,,}$

where ${\displaystyle i}$ is the angle from the initial plane of polarization to the optic axis of the lamina,  ${\displaystyle s}$ is the angle from the initial plane of polarization to the plane of polarization of the final ordinary image, and ${\displaystyle \phi }$ is the phase lag of the extraordinary wave relative to the ordinary wave due to the difference in propagation times through the lamina. The terms in ${\displaystyle \phi }$ are the frequency-dependent terms and explain why the lamina must be thin in order to produce discernible colors: if the lamina is too thick, ${\displaystyle \cos \phi }$ will pass through too many cycles as the frequency varies through the visible range, and the eye (which divides the visible spectrum into only three bands) will not be able to resolve the cycles.

From these equations it is easily verified that ${\displaystyle \,I_{o}+I_{e}=1\,}$ for all ${\displaystyle \phi ,}$ so that the colors are complementary. Without the phase-inversion rule, there would be a plus sign in front of the last term in the second equation, so that the ${\displaystyle \phi }$-dependent term would be the same in both equations, implying (incorrectly) that the colors were of the same hue.

These equations were included in an undated note that Fresnel gave to Biot,^[174] to which Biot added a few lines of his own. If we substitute

${\displaystyle U=\cos ^{2}{\tfrac {\phi }{2}}}$  and  ${\displaystyle A=\sin ^{2}{\tfrac {\phi }{2}}\,,}$

then Fresnel's formulae can be rewritten as

${\displaystyle \!I_{o}=U\cos ^{2}s+A\cos ^{2}(2i-s)\,,}$

${\displaystyle I_{e}=U\sin ^{2}s+A\sin ^{2}(2i-s)\,,}$

which are none other than Biot's empirical formulae of 1812,^[175] except that Biot interpreted ${\displaystyle U}$ and ${\displaystyle A}$ as the "unaffected" and "affected" selections of the rays incident on the lamina. If Biot's substitutions were accurate, they would imply that his experimental results were more fully explained by Fresnel's theory than by his own.

Arago delayed reporting on Fresnel's works on chromatic polarization until June 1821, when he used them in a broad attack on Biot's theory. In his written response, Biot protested that Arago's attack went beyond the proper scope of a report on the nominated works of Fresnel. But Biot also claimed that the substitutions for ${\displaystyle U}$ and ${\displaystyle A,}$ and therefore Fresnel's expressions for ${\displaystyle I_{o}}$ and ${\displaystyle I_{e},}$ were empirically wrong because when Fresnel's intensities of spectral colors were mixed according to Newton's rules, the squared cosine and sine functions varied too smoothly to account for the observed sequence of colors. That claim drew a written reply from Fresnel,^[176] who disputed whether the colors changed as abruptly as Biot claimed,^[177] and whether the human eye could judge color with sufficient objectivity for the purpose. On the latter question, Fresnel pointed out that different observers may give different names to the same color. Furthermore, he said, a single observer can only compare colors side by side; and even if they are judged to be the same, the identity is of sensation, not necessarily of composition.^[178] Fresnel's oldest and strongest point—that thin crystals were subject to the same laws as thick ones and did not need or allow a separate theory—Biot left unanswered.  Arago and Fresnel were seen to have won the debate.^[179]

Moreover, by this time Fresnel had a new, simpler explanation of his equations on chromatic polarization.

In the draft memoir of 30 August 1816, Fresnel mentioned two hypotheses—one of which he attributed to Ampère—by which the non-interference of orthogonally-polarized beams could be explained if polarized light waves were partly transverse. But Fresnel could not develop either of these ideas into a comprehensive theory. As early as September 1816, according to his later account,^[180] he realized that the non-interference of orthogonally-polarized beams, together with the phase-inversion rule in chromatic polarization, would be most easily explained if the waves were purely transverse, and Ampère "had the same thought" on the phase-inversion rule. But that would raise a new difficulty: as natural light seemed to be unpolarized and its waves were therefore presumed to be longitudinal, one would need to explain how the longitudinal component of vibration disappeared on polarization, and why it did not reappear when polarized light was reflected or refracted obliquely by a glass plate.^[181]

Independently, on 12 January 1817, Young wrote to Arago (in English) noting that a transverse vibration would constitute a polarization, and that if two longitudinal waves crossed at a significant angle, they could not cancel without leaving a residual transverse vibration.^[182] Young repeated this idea in an article published in a supplement to the Encyclopædia Britannica in February 1818, in which he added that Malus's law would be explained if polarization consisted in a transverse motion.^{[183]: 333–335}

Thus Fresnel, by his own testimony, may not have been the first person to suspect that light waves could have a transverse component, or that polarized waves were exclusively transverse. And it was Young, not Fresnel, who first published the idea that polarization depends on the orientation of a transverse vibration. But these incomplete theories had not reconciled the nature of polarization with the apparent existence of unpolarized light; that achievement was to be Fresnel's alone.

In a note that Buchwald dates in the summer of 1818, Fresnel entertained the idea that unpolarized waves could have vibrations of the same energy and obliquity, with their orientations distributed uniformly about the wave-normal, and that the degree of polarization was the degree of non-uniformity in the distribution. Two pages later he noted, apparently for the first time in writing, that his phase-inversion rule and the non-interference of orthogonally-polarized beams would be easily explained if the vibrations of fully polarized waves were "perpendicular to the normal to the wave"—that is, purely transverse.^[184]

But if he could account for lack of polarization by averaging out the transverse component, he did not also need to assume a longitudinal component. It was enough to suppose that light waves are purely transverse, hence always polarized in the sense of having a particular transverse orientation, and that the "unpolarized" state of natural or "direct" light is due to rapid and random variations in that orientation, in which case two coherent portions of "unpolarized" light will still interfere because their orientations will be synchronized.

It is not known exactly when Fresnel made this last step, because there is no relevant documentation from 1820 or early 1821 ^[185] (perhaps because he was too busy working on lighthouse-lens prototypes; see below). But he first published the idea in a paper on "Calcul des teintes…" ("calculation of the tints…"), serialized in Arago's Annales for May, June, and July 1821.^[186] In the first installment, Fresnel described "direct" (unpolarized) light as "the rapid succession of systems of waves polarized in all directions",^[187] and gave what is essentially the modern explanation of chromatic polarization, albeit in terms of the analogy between polarization and the resolution of forces in a plane, mentioning transverse waves only in a footnote. The introduction of transverse waves into the main argument was delayed to the second installment, in which he revealed the suspicion that he and Ampère had harbored since 1816, and the difficulty it raised.^[188] He continued:

It has only been for a few months that in meditating more attentively on this subject, I have realized that it was very probable that the oscillatory movements of light waves were executed solely along the plane of these waves, for direct light as well as for polarized light.^{[189][Note 6]}

According to this new view, he wrote, "the act of polarization consists not in creating these transverse movements, but in decomposing them into two fixed perpendicular directions and in separating the two components".^[190]

While selectionists could insist on interpreting Fresnel's diffraction integrals in terms of discrete, countable rays, they could not do the same with his theory of polarization. For a selectionist, the state of polarization of a beam concerned the distribution of orientations over the population of rays, and that distribution was presumed to be static. For Fresnel, the state of polarization of a beam concerned the variation of a displacement over time. That displacement might be constrained but was not static, and rays were geometric constructions, not countable objects. The conceptual gap between the wave theory and selectionism had become unbridgeable.^[191]

The other difficulty posed by pure transverse waves, of course, was the apparent implication that the aether was an elastic solid, except that, unlike other elastic solids, it was incapable of transmitting longitudinal waves.^{[Note 7]} The wave theory was cheap on assumptions, but its latest assumption was expensive on credulity.^[192] If that assumption was to be widely entertained, its explanatory power would need to be impressive.

In the second installment of "Calcul des teintes" (June 1821), Fresnel supposed, by analogy with sound waves, that the density of the aether in a refractive medium was inversely proportional to the square of the wave velocity, and therefore directly proportional to the square of the refractive index. For reflection and refraction at the surface between two isotropic media of different indices, Fresnel decomposed the transverse vibrations into two perpendicular components, now known as the s and p components, which are parallel to the surface and the plane of incidence, respectively; in other words, the s and p components are respectively square and parallel to the plane of incidence.^{[Note 8]} For the s component, Fresnel supposed that the interaction between the two media was analogous to an elastic collision, and obtained a formula for what we now call the reflectivity: the ratio of the reflected intensity to the incident intensity. The predicted reflectivity was non-zero at all angles.^[193]

The third installment (July 1821) was a short "postscript" in which Fresnel announced that he had found, by a "mechanical solution", a formula for the reflectivity of the p component, which predicted that the reflectivity was zero at the Brewster angle. So polarization by reflection had been accounted for—but with the proviso that the direction of vibration in Fresnel's model was perpendicular to the plane of polarization as defined by Malus. (On the ensuing controversy, see Plane of polarization.) The technology of the time did not allow the s and p reflectivities to be measured accurately enough to test Fresnel's formulae at arbitrary angles of incidence. But the formulae could be rewritten in terms of what we now call the reflection coefficient: the signed ratio of the reflected amplitude to the incident amplitude. Then, if the plane of polarization of the incident ray was at 45° to the plane of incidence, the tangent of the corresponding angle for the reflected ray was obtainable from the ratio of the two reflection coefficients, and this angle could be measured. Fresnel had measured it for a range of angles of incidence, for glass and water, and the agreement between the calculated and measured angles was better than 1.5° in all cases.^[194]

Fresnel gave details of the "mechanical solution" in a memoir read to the Académie des Sciences on 7 January 1823.^[195] Conservation of energy was combined with continuity of the tangential vibration at the interface.^[196] The resulting formulae for the reflection coefficients and reflectivities became known as the Fresnel equations. The reflection coefficients for the s and p polarizations are most succinctly expressed as

${\displaystyle r_{s}=-{\frac {\sin(i-r)}{\sin(i+r)}}}$    and    ${\displaystyle r_{p}={\frac {\tan(i-r)}{\tan(i+r)}}\,,}$

where ${\displaystyle i}$ and ${\displaystyle r}$ are the angles of incidence and refraction; these equations are known respectively as Fresnel's sine law and Fresnel's tangent law.^[197] By allowing the coefficients to be complex, Fresnel even accounted for the different phase shifts of the s and p components due to total internal reflection.^[198]

This success inspired James MacCullagh and Augustin-Louis Cauchy, beginning in 1836, to analyze reflection from metals by using the Fresnel equations with a complex refractive index.^[199] The same technique is applicable to non-metallic opaque media. With these generalizations, the Fresnel equations can predict the appearance of a wide variety of objects under illumination—for example, in computer graphics (see Physically based rendering).

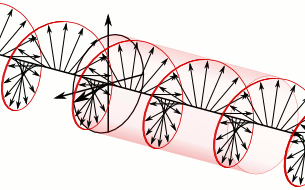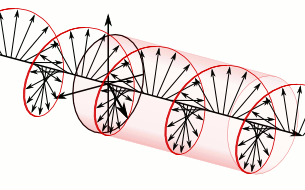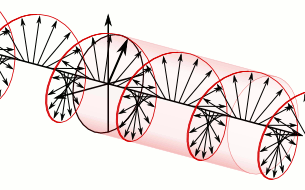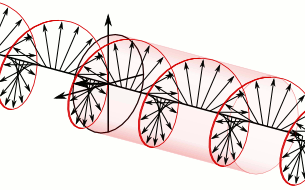
In a memoir dated 9 December 1822,^[200] Fresnel coined the terms linear polarization (French: polarisation rectiligne) for the simple case in which the perpendicular components of vibration are in phase or 180° out of phase, circular polarization for the case in which they are of equal magnitude and a quarter-cycle (±90°) out of phase, and elliptical polarization for other cases in which the two components have a fixed amplitude ratio and a fixed phase difference. He then explained how optical rotation could be understood as a species of birefringence. Linearly-polarized light could be resolved into two circularly-polarized components rotating in opposite directions. If these components propagated at slightly different speeds, the phase difference between them—and therefore the direction of their linearly-polarized resultant—would vary continuously with distance.^[201]

These concepts called for a redefinition of the distinction between polarized and unpolarized light. Before Fresnel, it was thought that polarization could vary in direction, and in degree (e.g., due to variation in the angle of reflection off a transparent body), and that it could be a function of color (chromatic polarization), but not that it could vary in kind. Hence it was thought that the degree of polarization was the degree to which the light could be suppressed by an analyzer with the appropriate orientation. Light that had been converted from linear to elliptical or circular polarization (e.g., by passage through a crystal lamina, or by total internal reflection) was described as partly or fully "depolarized" because of its behavior in an analyzer. After Fresnel, the defining feature of polarized light was that the perpendicular components of vibration had a fixed ratio of amplitudes and a fixed difference in phase. By that definition, elliptically or circularly polarized light is fully polarized although it cannot be fully suppressed by an analyzer alone.^[202] The conceptual gap between the wave theory and selectionism had widened again.

By 1817 it had been discovered by Brewster,^[203] but not adequately reported,^{[204][183]: 324} that plane-polarized light was partly depolarized by total internal reflection if initially polarized at an acute angle to the plane of incidence. Fresnel rediscovered this effect and investigated it by including total internal reflection in a chromatic-polarization experiment. With the aid of his first theory of chromatic polarization, he found that the apparently depolarized light was a mixture of components polarized parallel and perpendicular to the plane of incidence, and that the total reflection introduced a phase difference between them.^[205] Choosing an appropriate angle of incidence (not yet exactly specified) gave a phase difference of 1/8 of a cycle (45°). Two such reflections from the "parallel faces" of "two coupled prisms" gave a phase difference of 1/4 of a cycle (90°). These findings were contained in a memoir submitted to the Académie on 10 November 1817 and read a fortnight later. An undated marginal note indicates that the two coupled prisms were later replaced by a single "parallelepiped in glass"—now known as a Fresnel rhomb.^[206]

This was the memoir whose "supplement",^[133] dated January 1818, contained the method of superposing sinusoidal functions and the restatement of Malus's law in terms of amplitudes. In the same supplement, Fresnel reported his discovery that optical rotation could be emulated by passing the polarized light through a Fresnel rhomb (still in the form of "coupled prisms"), followed by an ordinary birefringent lamina sliced parallel to its axis, with the axis at 45° to the plane of reflection of the Fresnel rhomb, followed by a second Fresnel rhomb at 90° to the first.^[207] In a further memoir read on 30 March,^[208] Fresnel reported that if polarized light was fully "depolarized" by a Fresnel rhomb—now described as a parallelepiped—its properties were not further modified by a subsequent passage through an optically rotating medium or device.

The connection between optical rotation and birefringence was further explained in 1822, in the memoir on elliptical and circular polarization.^[200] This was followed by the memoir on reflection, read in January 1823, in which Fresnel quantified the phase shifts in total internal reflection, and thence calculated the precise angle at which a Fresnel rhomb should be cut in order to convert linear polarization to circular polarization. For a refractive index of 1.51, there were two solutions: about 48.6° and 54.6°.^[195]: 760

When light passes through a slice of calcite cut perpendicular to its optic axis, the difference between the propagation times of the ordinary and extraordinary waves has a second-order dependence on the angle of incidence. If the slice is observed in a highly convergent cone of light, that dependence becomes significant, so that a chromatic-polarization experiment will show a pattern of concentric rings. But most minerals, when observed in this manner, show a more complicated pattern of rings involving two foci and a lemniscate curve, as if they had two optic axes.^[209][210] The two classes of minerals naturally become known as uniaxal and biaxal—or, in later literature, uniaxial and biaxial.

In 1813, Brewster observed the simple concentric pattern in "beryl, emerald, ruby &c." The same pattern was later observed in calcite by Wollaston, Biot, and Seebeck.  Biot, assuming that the concentric pattern was the general case, tried to calculate the colors with his theory of chromatic polarization, and succeeded better for some minerals than for others. In 1818, Brewster belatedly explained why: seven of the twelve minerals employed by Biot had the lemniscate pattern, which Brewster had observed as early as 1812; and the minerals with the more complicated rings also had a more complicated law of refraction.^[211]

In a uniform crystal, according to Huygens's theory, the secondary wavefront that expands from the origin in unit time is the ray-velocity surface—that is, the surface whose "distance" from the origin in any direction is the ray velocity in that direction. In calcite, this surface is two-sheeted, consisting of a sphere (for the ordinary wave) and an oblate spheroid (for the extraordinary wave) touching each other at opposite points of a common axis—touching at the north and south poles, if we may use a geographic analogy. But according to Malus's corpuscular theory of double refraction, the ray velocity was proportional to the reciprocal of that given by Huygens's theory, in which case the velocity law was of the form

${\displaystyle v_{o}^{2\!}-v_{e}^{2}=k\sin ^{2}\theta \,,}$

where ${\displaystyle v_{o}}$ and ${\displaystyle v_{e}}$ were the ordinary and extraordinary ray velocities according to the corpuscular theory, and ${\displaystyle \theta }$ was the angle between the ray and the optic axis.^[212] By Malus's definition, the plane of polarization of a ray was the plane of the ray and the optic axis if the ray was ordinary, or the perpendicular plane (containing the ray) if the ray was extraordinary. In Fresnel's model, the direction of vibration was normal to the plane of polarization. Hence, for the sphere (the ordinary wave), the vibration was along the lines of latitude (continuing the geographic analogy); and for the spheroid (the extraordinary wave), the vibration was along the lines of longitude.

On 29 March 1819,^[213] Biot presented a memoir in which he proposed simple generalizations of Malus's rules for a crystal with two axes, and reported that both generalizations seemed to be confirmed by experiment. For the velocity law, the squared sine was replaced by the product of the sines of the angles from the ray to the two axes (Biot's sine law). And for the polarization of the ordinary ray, the plane of the ray and the axis was replaced by the plane bisecting the dihedral angle between the two planes each of which contained the ray and one axis (Biot's dihedral law).^[214][215] Biot's laws meant that a biaxial crystal with axes at a small angle, cleaved in the plane of those axes, behaved nearly like a uniaxial crystal at near-normal incidence; this was fortunate because gypsum, which had been used in chromatic-polarization experiments, is biaxial.^[216]

Until Fresnel turned his attention to biaxial birefringence, it was assumed that one of the two refractions was ordinary, even in biaxial crystals.^[217] But, in a memoir submitted ^{[Note 9]} on 19 November 1821,^[218] Fresnel reported two experiments on topaz showing that neither refraction was ordinary in the sense of satisfying Snell's law; that is, neither ray was the product of spherical secondary waves.^[219]

The same memoir contained Fresnel's first attempt at the biaxial velocity law. For calcite, if we interchange the equatorial and polar radii of Huygens's oblate spheroid while preserving the polar direction, we obtain a prolate spheroid touching the sphere at the equator. A plane through the center/origin cuts this prolate spheroid in an ellipse whose major and minor semi-axes give the magnitudes of the extraordinary and ordinary ray velocities in the direction normal to the plane, and (said Fresnel) the directions of their respective vibrations. The direction of the optic axis is the normal to the plane for which the ellipse of intersection reduces to a circle. So, for the biaxial case, Fresnel simply replaced the prolate spheroid with a triaxial ellipsoid,^[220] which was to be sectioned by a plane in the same way. In general there would be two planes passing through the center of the ellipsoid and cutting it in a circle, and the normals to these planes would give two optic axes. From the geometry, Fresnel deduced Biot's sine law (with the ray velocities replaced by their reciprocals).^[221]

The ellipsoid indeed gave the correct ray velocities (although the initial experimental verification was only approximate). But it did not give the correct directions of vibration, for the biaxial case or even for the uniaxial case, because the vibrations in Fresnel's model were tangential to the wavefront—which, for an extraordinary ray, is not generally normal to the ray. This error (which is small if, as in most cases, the birefringence is weak) was corrected in an "extract" that Fresnel read to the Académie a week later, on 26 November. Starting with Huygens's spheroid, Fresnel obtained a 4th-degree surface which, when sectioned by a plane as above, would yield the wave-normal velocities for a wavefront in that plane, together with their vibration directions. For the biaxial case, he generalized the equation to obtain a surface with three unequal principal dimensions; this he subsequently called the "surface of elasticity". But he retained the earlier ellipsoid as an approximation, from which he deduced Biot's dihedral law.^[222]

Fresnel's initial derivation of the surface of elasticity had been purely geometric, and not deductively rigorous. His first attempt at a mechanical derivation, contained in a "supplement" dated 13 January 1822, assumed that (i) there were three mutually perpendicular directions in which a displacement produced a reaction in the same direction, (ii) the reaction was otherwise a linear function of the displacement, and (iii) the radius of the surface in any direction was the square root of the component, in that direction, of the reaction to a unit displacement in that direction. The last assumption recognized the requirement that if a wave was to maintain a fixed direction of propagation and a fixed direction of vibration, the reaction must not be outside the plane of those two directions.^[223]

In the same supplement, Fresnel considered how he might find, for the biaxial case, the secondary wavefront that expands from the origin in unit time—that is, the surface that reduces to Huygens's sphere and spheroid in the uniaxial case. He noted that this "wave surface" (surface de l'onde)^[224] is tangential to all possible plane wavefronts that could have crossed the origin one unit of time ago, and he listed the mathematical conditions that it must satisfy. But he doubted the feasibility of deriving the surface from those conditions.^[225]

In a "second supplement",^[226] Fresnel eventually exploited two related facts: (i) the "wave surface" was also the ray-velocity surface, which could be obtained by sectioning the ellipsoid that he had initially mistaken for the surface of elasticity, and (ii) the "wave surface" intersected each plane of symmetry of the ellipsoid in two curves: a circle and an ellipse. Thus he found that the "wave surface" is described by the 4th-degree equation

${\displaystyle r^{2}{\big (}a^{2}x^{2\!}+b^{2}y^{2\!}+c^{2}z^{2}{\big )}-a^{2}{\big (}b^{2\!}+c^{2}{\big )}x^{2}-b^{2}{\big (}c^{2\!}+a^{2}{\big )}y^{2}-c^{2}{\big (}a^{2\!}+b^{2}{\big )}z^{2}+a^{2}b^{2}c^{2}=\,0\,,}$

where ${\displaystyle \,r^{2}=x^{2\!}+y^{2\!}+z^{2},\,}$ and ${\displaystyle \,a,b,c\,}$ are the propagation speeds in directions normal to the coordinate axes for vibrations along the axes (the ray and wave-normal speeds being the same in those special cases).^[227] Later commentators^[228]: 19 put the equation in the more compact and memorable form

${\displaystyle {\frac {x^{2}}{r^{2}-a^{2}}}+{\frac {y^{2}}{r^{2}-b^{2}}}+{\frac {z^{2}}{r^{2}-c^{2}}}\,=\,1\,.}$

Earlier in the "second supplement", Fresnel modeled the medium as an array of point-masses and found that the force-displacement relation was described by a symmetric matrix, confirming the existence of three mutually perpendicular axes on which the displacement produced a parallel force.^[229] Later in the document, he noted that in a biaxial crystal, unlike a uniaxial crystal, the directions in which there is only one wave-normal velocity are not the same as those in which there is only one ray velocity.^[230] Nowadays we refer to the former directions as the optic axes or binormal axes, and the latter as the ray axes or biradial axes (see Birefringence).^[231]

Fresnel's "second supplement" was signed on 31 March 1822 and submitted the next day—less than a year after the publication of his pure-transverse-wave hypothesis, and just less than a year after the demonstration of his prototype eight-panel lighthouse lens (see below).

Having presented the pieces of his theory in roughly the order of discovery, Fresnel needed to rearrange the material so as to emphasize the mechanical foundations;^[232] and he still needed a rigorous treatment of Biot's dihedral law.^[233] He attended to these matters in his "second memoir" on double refraction,^[234] published in the Recueils of the Académie des Sciences for 1824; this was not actually printed until late 1827, a few months after his death.^[235] In this work, having established the three perpendicular axes on which a displacement produces a parallel reaction,^[236] and thence constructed the surface of elasticity,^[237] he showed that Biot's dihedral law is exact provided that the binormals are taken as the optic axes, and the wave-normal direction as the direction of propagation.^[238]

As early as 1822, Fresnel discussed his perpendicular axes with Cauchy. Acknowledging Fresnel's influence, Cauchy went on to develop the first rigorous theory of elasticity of non-isotropic solids (1827), hence the first rigorous theory of transverse waves therein (1830)—which he promptly tried to apply to optics.^[239] The ensuing difficulties drove a long competitive effort to find an accurate mechanical model of the aether.^[240] Fresnel's own model was not dynamically rigorous; for example, it deduced the reaction to a shear strain by considering the displacement of one particle while all others were fixed, and it assumed that the stiffness determined the wave velocity as in a stretched string, whatever the direction of the wave-normal. But it was enough to enable the wave theory to do what selectionist theory could not: generate testable formulae covering a comprehensive range of optical phenomena, from mechanical assumptions.^[241]

In 1815, Brewster reported that colors appear when a slice of isotropic material, placed between crossed polarizers, is mechanically stressed. Brewster himself immediately and correctly attributed this phenomenon to stress-induced birefringence ^[242][243]—now known as photoelasticity.

In a memoir read in September 1822, Fresnel announced that he had verified Brewster's diagnosis more directly, by compressing a combination of glass prisms so severely that one could actually see a double image through it. In his experiment, Fresnel lined up seven 45°–90°–45° prisms, short side to short side, with their 90° angles pointing in alternating directions. Two half-prisms were added at the ends to make the whole assembly rectangular. The prisms were separated by thin films of turpentine (térébenthine) to suppress internal reflections, allowing a clear line of sight along the row. When the four prisms with similar orientations were compressed in a vise across the line of sight, an object viewed through the assembly produced two images with perpendicular polarizations, with an apparent spacing of 1.5 mm at one metre.^[244][245]

At the end of that memoir, Fresnel predicted that if the compressed prisms were replaced by (unstressed) monocrystalline quartz prisms with matching directions of optical rotation, and with their optic axes aligned along the row, an object seen by looking along the common optic axis would give two images, which would seem unpolarized when viewed through an analyzer but, when viewed through a Fresnel rhomb, would be polarized at ±45° to the plane of reflection of the rhomb (indicating that they were initially circularly polarized in opposite directions). This would show directly that optical rotation is a form of birefringence. In the memoir of December 1822, in which he introduced the term circular polarization, he reported that he had confirmed this prediction using only one 14°–152°–14° prism and two glass half-prisms. But he obtained a wider separation of the images by replacing the glass half-prism with quartz half-prisms whose rotation was opposite to that of the 14°–152°–14° prism. He added in passing that one could further increase the separation by increasing the number of prisms.^[246]

For the supplement to Riffault's translation of Thomson's System of Chemistry, Fresnel was chosen to contribute the article on light. The resulting 137-page essay, titled De la Lumière (On Light),^[247] was apparently finished in June 1821 and published by February 1822.^[248] With sections covering the nature of light, diffraction, thin-film interference, reflection and refraction, double refraction and polarization, chromatic polarization, and modification of polarization by reflection, it made a comprehensive case for the wave theory to a readership that was not restricted to physicists.^[249]

To examine Fresnel's first memoir and supplements on double refraction, the Académie des Sciences appointed Ampère, Arago, Fourier, and Poisson.^[250] Their report,^[251] of which Arago was clearly the main author,^[252] was delivered at the meeting of 19 August 1822. Then, in the words of Émile Verdet, as translated by Ivor Grattan-Guinness:

Immediately after the reading of the report, Laplace took the floor, and… proclaimed the exceptional importance of the work which had just been reported: he congratulated the author on his steadfastness and his sagacity which had led him to discover a law which had escaped the cleverest, and, anticipating somewhat the judgement of posterity, declared that he placed these researches above everything that had been communicated to the Académie for a long time.^[253]

Whether Laplace was announcing his conversion to the wave theory—at the age of 73—is uncertain. Grattan-Guinness entertained the idea.^[254] Buchwald, noting that Arago failed to explain that the "ellipsoid of elasticity" did not give the correct planes of polarization, suggests that Laplace may have merely regarded Fresnel's theory as a successful generalization of Malus's ray-velocity law, embracing Biot's laws.^[255]

In the following year, Poisson, who did not sign Arago's report, disputed the possibility of transverse waves in the aether. Starting from assumed equations of motion of a fluid medium, he noted that they did not give the correct results for partial reflection and double refraction—as if that were Fresnel's problem rather than his own—and that the predicted waves, even if they were initially transverse, became more longitudinal as they propagated. In reply Fresnel noted, inter alia, that the equations in which Poisson put so much faith did not even predict viscosity. The implication was clear: given that the behavior of light had not been satisfactorily explained except by transverse waves, it was not the responsibility of the wave-theorists to abandon transverse waves in deference to pre-conceived notions about the aether; rather, it was the responsibility of the aether modelers to produce a model that accommodated transverse waves.^[256] According to Robert H. Silliman, Poisson eventually accepted the wave theory shortly before his death in 1840.^[257]

Among the French, Poisson's reluctance was an exception. According to Eugene Frankel, "in Paris no debate on the issue seems to have taken place after 1825. Indeed, almost the entire generation of physicists and mathematicians who came to maturity in the 1820s—Pouillet, Savart, Lamé, Navier, Liouville, Cauchy—seem to have adopted the theory immediately." Fresnel's other prominent French opponent, Biot, appeared to take a neutral position in 1830, and eventually accepted the wave theory—possibly by 1846 and certainly by 1858.^[258]

In 1826, the British astronomer John Herschel, who was working on a book-length article on light for the Encyclopædia Metropolitana, addressed three questions to Fresnel concerning double refraction, partial reflection, and their relation to polarization. The resulting article,^[259] titled simply "Light", was highly sympathetic to the wave theory, although not entirely free of selectionist language. It was circulating privately by 1828 and was published in 1830.^[260] Meanwhile, Young's translation of Fresnel's De la Lumière was published in installments from 1827 to 1829.^[261] George Biddell Airy, the former Lucasian Professor at Cambridge and future Astronomer Royal, unreservedly accepted the wave theory by 1831.^[262] In 1834, he famously calculated the diffraction pattern of a circular aperture from the wave theory,^[263] thereby explaining the limited angular resolution of a perfect telescope (see Airy disk). By the end of the 1830s, the only prominent British physicist who held out against the wave theory was Brewster, whose objections included the difficulty of explaining photochemical effects and (in his opinion) dispersion.^[264]

A German translation of De la Lumière was published in installments in 1825 and 1828. The wave theory was adopted by Fraunhofer in the early 1820s and by Franz Ernst Neumann in the 1830s, and then began to find favor in German textbooks.^[265]

The economy of assumptions under the wave theory was emphasized by William Whewell in his History of the Inductive Sciences, first published in 1837. In the corpuscular system, "every new class of facts requires a new supposition," whereas in the wave system, a hypothesis devised in order to explain one phenomenon is then found to explain or predict others. In the corpuscular system there is "no unexpected success, no happy coincidence, no convergence of principles from remote quarters"; but in the wave system, "all tends to unity and simplicity." ^[266]

Hence, in 1850, when Foucault and Fizeau found by experiment that light travels more slowly in water than in air, in accordance with the wave explanation of refraction and contrary to the corpuscular explanation, the result came as no surprise.^[267]

Fresnel was not the first person to focus a lighthouse beam using a lens. That distinction apparently belongs to the London glass-cutter Thomas Rogers, whose first lenses, 53 cm in diameter and 14 cm thick at the center, were installed at the Old Lower Lighthouse at Portland Bill in 1789. Further samples were installed in about half a dozen other locations by 1804. But much of the light was wasted by absorption in the glass.^[268][269]

Nor was Fresnel the first to suggest replacing a convex lens with a series of concentric annular prisms, to reduce weight and absorption. In 1748, Count Buffon proposed grinding such prisms as steps in a single piece of glass.^[4] In 1790,^[271] the Marquis de Condorcet suggested that it would be easier to make the annular sections separately and assemble them on a frame; but even that was impractical at the time.^[272][273] These designs were intended not for lighthouses,^[4] but for burning glasses.^[274]: 609 Brewster, however, proposed a system similar to Condorcet's in 1811,^{[4][275][132]} and by 1820 was advocating its use in British lighthouses.^[276]

Meanwhile, on 21 June 1819, Fresnel was "temporarily" seconded by the Commission des Phares (Commission of Lighthouses) on the recommendation of Arago (a member of the Commission since 1813), to review possible improvements in lighthouse illumination.^[277][272] The commission had been established by Napoleon in 1811 and placed under the Corps des Ponts—Fresnel's employer.^[278]

By the end of August 1819, unaware of the Buffon-Condorcet-Brewster proposal,^[272][132] Fresnel made his first presentation to the commission,^[279] recommending what he called lentilles à échelons (lenses by steps) to replace the reflectors then in use, which reflected only about half of the incident light.^{[280][Note 10]} One of the assembled commissioners, Jacques Charles, recalled Buffon's suggestion, leaving Fresnel embarrassed for having again "broken through an open door".^[270] But, whereas Buffon's version was biconvex and in one piece, Fresnel's was plano-convex and made of multiple prisms for easier construction. With an official budget of 500 francs, Fresnel approached three manufacturers. The third, François Soleil, produced the prototype. Finished in March 1820, it had a square lens panel 55 cm on a side, containing 97 polygonal (not annular) prisms—and so impressed the Commission that Fresnel was asked for a full eight-panel version. This model, completed a year later in spite of insufficient funding, had panels 76 cm square. In a public spectacle on the evening of 13 April 1821, it was demonstrated by comparison with the most recent reflectors, which it suddenly rendered obsolete.^[281]

Fresnel's next lens was a rotating apparatus with eight "bull's-eye" panels, made in annular arcs by Saint-Gobain,^[273] giving eight rotating beams—to be seen by mariners as a periodic flash. Above and behind each main panel was a smaller, sloping bull's-eye panel of trapezoidal outline with trapezoidal elements.^[282] This refracted the light to a sloping plane mirror, which then reflected it horizontally, 7 degrees ahead of the main beam, increasing the duration of the flash.^[283] Below the main panels were 128 small mirrors arranged in four rings, stacked like the slats of a louver or Venetian blind. Each ring, shaped as a frustum of a cone, reflected the light to the horizon, giving a fainter steady light between the flashes. The official test, conducted on the unfinished Arc de Triomphe on 20 August 1822, was witnessed by the commission—and by Louis XVIII and his entourage—from 32 km away. The apparatus was stored at Bordeaux for the winter, and then reassembled at Cordouan Lighthouse under Fresnel's supervision. On 25 July 1823, the world's first lighthouse Fresnel lens was lit.^[284] Soon afterwards, Fresnel started coughing up blood.^[285]

In May 1824,^[132] Fresnel was promoted to secretary of the Commission des Phares, becoming the first member of that body to draw a salary,^[286] albeit in the concurrent role of Engineer-in-Chief.^[287] He was also an examiner (not a teacher) at the École Polytechnique since 1821; but poor health, long hours during the examination season, and anxiety about judging others induced him to resign that post in late 1824, to save his energy for his lighthouse work.^[34][288]

In the same year he designed the first fixed lens—for spreading light evenly around the horizon while minimizing waste above or below.^[272] Ideally the curved refracting surfaces would be segments of toroids about a common vertical axis, so that the dioptric panel would look like a cylindrical drum. If this was supplemented by reflecting (catoptric) rings above and below the refracting (dioptric) parts, the entire apparatus would look like a beehive.^[289] The second Fresnel lens to enter service was indeed a fixed lens, of third order, installed at Dunkirk by 1 February 1825.^[290] However, due to the difficulty of fabricating large toroidal prisms, this apparatus had a 16-sided polygonal plan.^[291]

In 1825, Fresnel extended his fixed-lens design by adding a rotating array outside the fixed array. Each panel of the rotating array was to refract part of the fixed light from a horizontal fan into a narrow beam.^[272][292]

Also in 1825, Fresnel unveiled the Carte des Phares (Lighthouse Map), calling for a system of 51 lighthouses plus smaller harbor lights, in a hierarchy of lens sizes (called orders, the first order being the largest), with different characteristics to facilitate recognition: a constant light (from a fixed lens), one flash per minute (from a rotating lens with eight panels), and two per minute (sixteen panels).^[293]

In late 1825,^[294] to reduce the loss of light in the reflecting elements, Fresnel proposed to replace each mirror with a catadioptric prism, through which the light would travel by refraction through the first surface, then total internal reflection off the second surface, then refraction through the third surface.^[295] The result was the lighthouse lens as we now know it. In 1826 he assembled a small model for use on the Canal Saint-Martin,^[296] but he did not live to see a full-sized version.

The first fixed lens with toroidal prisms was a first-order apparatus designed by the Scottish engineer Alan Stevenson under the guidance of Léonor Fresnel, and fabricated by Isaac Cookson & Co. from French glass; it entered service at the Isle of May in 1836.^[297] The first large catadioptric lenses were fixed third-order lenses made in 1842 for the lighthouses at Gravelines and Île Vierge. The first fully catadioptric first-order lens, installed at Ailly in 1852, gave eight rotating beams assisted by eight catadioptric panels at the top (to lengthen the flashes), plus a fixed light from below. The first fully catadioptric lens with purely revolving beams—also of first order—was installed at Saint-Clément-des-Baleines in 1854, and marked the completion of Augustin Fresnel's original Carte des Phares.^[298]

Production of one-piece stepped dioptric lenses—roughly as envisaged by Buffon—became practical in 1852, when John L. Gilliland of the Brooklyn Flint-Glass Company patented a method of making such lenses from press-molded glass.^[299] By the 1950s, the substitution of plastic for glass made it economic to use fine-stepped Fresnel lenses as condensers in overhead projectors.^[300] Still finer steps can be found in low-cost plastic "sheet" magnifiers.

Fresnel was elected to the Société Philomathique de Paris in April 1819,^[301] and in 1822 became one of the editors of the Société's  Bulletin des Sciences.^[302] As early as May 1817, at Arago's suggestion, Fresnel applied for membership of the Académie des Sciences, but received only one vote.^[301] The successful candidate on that occasion was Joseph Fourier. In November 1822, Fourier's elevation to Permanent Secretary of the Académie created a vacancy in the physics section, which was filled in February 1823 by Pierre Louis Dulong, with 36 votes to Fresnel's 20. But in May 1823, after another vacancy was left by the death of Jacques Charles,  Fresnel's election was unanimous.^[303] In 1824,^[304] Fresnel was made a chevalier de la Légion d'honneur (Knight of the Legion of Honour).^[9]

Meanwhile, in Britain, the wave theory was yet to take hold; Fresnel wrote to Thomas Young in November 1824, saying in part:

I am far from denying the value that I attach to the praise of English scholars, or pretending that they would not have flattered me agreeably. But for a long time this sensibility, or vanity, which is called the love of glory, has been much blunted in me: I work far less to capture the public's votes than to obtain an inner approbation which has always been the sweetest reward of my efforts. Doubtless I have often needed the sting of vanity to excite me to pursue my researches in moments of disgust or discouragement; but all the compliments I received from MM. Arago, Laplace, and Biot never gave me as much pleasure as the discovery of a theoretical truth and the confirmation of my calculations by experiment.^[305]

But "the praise of English scholars" soon followed. On 9 June 1825, Fresnel was made a Foreign Member of the Royal Society of London.^[306] In 1827^[25][307] he was awarded the society's Rumford Medal for the year 1824, "For his Development of the Undulatory Theory as applied to the Phenomena of Polarized Light, and for his various important discoveries in Physical Optics." ^[308]

A monument to Fresnel at his birthplace^[7][10] (see above)  was dedicated on 14 September 1884^[8] with a speech by Jules Jamin, Permanent Secretary of the Académie des Sciences.^[9][309]  "FRESNEL" is among the 72 names embossed on the Eiffel Tower (on the south-east side, fourth from the left). In the 19th century, as every lighthouse in France acquired a Fresnel lens, every one acquired a bust of Fresnel, seemingly watching over the coastline that he had made safer.^[310] The lunar features Promontorium Fresnel and Rimae Fresnel were later named after him.^[311]

Fresnel's health, which had always been poor, deteriorated in the winter of 1822–1823, increasing the urgency of his original research, and (in part) preventing him from contributing an article on polarization and double refraction for the Encyclopædia Britannica.^[312] The memoirs on circular and elliptical polarization and optical rotation,^[200] and on the detailed derivation of the Fresnel equations and their application to total internal reflection,^[195] date from this period. In the spring he recovered enough, in his own view, to supervise the lens installation at Cordouan. Soon afterwards, it became clear that his condition was tuberculosis.^[285]

In 1824, he was advised that if he wanted to live longer, he needed to scale back his activities. Perceiving his lighthouse work to be his most important duty, he resigned as an examiner at the École Polytechnique, and closed his scientific notebooks. His last note to the Académie, read on 13 June 1825, described the first radiometer and attributed the observed repulsive force to a temperature difference.^[313] Although his fundamental research ceased, his advocacy did not; as late as August or September 1826, he found the time to answer Herschel's queries on the wave theory.^[314] It was Herschel who recommended Fresnel for the Royal Society's Rumford Medal.^[315]

Fresnel's cough worsened in the winter of 1826–1827, leaving him too ill to return to Mathieu in the spring. The Académie meeting of 30 April 1827 was the last that he attended. In early June he was carried to Ville-d'Avray, 12 kilometres (7.5 mi) west of Paris. There his mother joined him. On 6 July, Arago arrived to deliver the Rumford Medal. Sensing Arago's distress, Fresnel whispered that "the most beautiful crown means little, when it is laid on the grave of a friend." Fresnel did not have the strength to reply to the Royal Society. He died eight days later, on Bastille Day.^[316]

He is buried at Père Lachaise Cemetery, Paris. The inscription on his headstone is partly eroded away; the legible part says, when translated, "To the memory of Augustin Jean Fresnel, member of the Institute of France".

Fresnel's "second memoir" on double refraction^[234] was not printed until late 1827, a few months after his death.^[317] Until then, the best published source on his work on double refraction was an extract of that memoir, printed in 1822.^[318] His final treatment of partial reflection and total internal reflection,^[195] read to the Académie in January 1823, was thought to be lost until it was rediscovered among the papers of the deceased Joseph Fourier (1768–1830), and was printed in 1831. Until then, it was known chiefly through an extract printed in 1823 and 1825. The memoir introducing the parallelepiped form of the Fresnel rhomb,^[319] read in March 1818, was mislaid until 1846,^[320] and then attracted such interest that it was soon republished in English.^[321] Most of Fresnel's writings on polarized light before 1821—including his first theory of chromatic polarization (submitted 7 October 1816) and the crucial "supplement" of January 1818 ^[133]—were not published in full until his Oeuvres complètes ("complete works") began to appear in 1866.^[322] The "supplement" of July 1816, proposing the "efficacious ray" and reporting the famous double-mirror experiment, met the same fate,^[323] as did the "first memoir" on double refraction.^[324]

Publication of Fresnel's collected works was itself delayed by the deaths of successive editors. The task was initially entrusted to Félix Savary, who died in 1841. It was restarted twenty years later by the Ministry of Public Instruction. Of the three editors eventually named in the Oeuvres, Sénarmont died in 1862, Verdet in 1866, and Léonor Fresnel in 1869, by which time only two of the three volumes had appeared.^[325] At the beginning of vol. 3 (1870), the completion of the project is described in a long footnote by "J. Lissajous."

Not included in the Oeuvres ^[326] are two short notes by Fresnel on magnetism, which were discovered among Ampère's manuscripts.^[327]: 104 In response to Ørsted's discovery of electromagnetism in 1820, Ampère initially supposed that the field of a permanent magnet was due to a macroscopic circulating current. Fresnel suggested instead that there was a microscopic current circulating around each particle of the magnet. In his first note, he argued that microscopic currents, unlike macroscopic currents, would explain why a hollow cylindrical magnet does not lose its magnetism when cut longitudinally. In his second note, dated 5 July 1821, he further argued that a macroscopic current had the counterfactual implication that a permanent magnet should be hot, whereas microscopic currents circulating around the molecules might avoid the heating mechanism.^{[327]: 101–104} He was not to know that the fundamental units of permanent magnetism are even smaller than molecules (see Electron magnetic moment). The two notes, together with Ampère's acknowledgment, were eventually published in 1885.^[328]

Fresnel's essay Rêveries of 1814 has not survived.^[329] The article "Sur les Différents Systèmes relatifs à la Théorie de la Lumière" ("On the Different Systems relating to the Theory of Light"), which Fresnel wrote for the newly launched English journal European Review,^[330] was received by the publisher's agent in Paris in September 1824. The journal failed before Fresnel's contribution could be published. Fresnel tried unsuccessfully to recover the manuscript. The editors of his collected works were unable to find it, and concluded that it was probably lost.^[331]

In 1810, Arago found experimentally that the degree of refraction of starlight does not depend on the direction of the earth's motion relative to the line of sight. In 1818, Fresnel showed that this result could be explained by the wave theory,^[332] on the hypothesis that if an object with refractive index ${\displaystyle n}$ moved at velocity ${\displaystyle v}$ relative to the external aether (taken as stationary), then the velocity of light inside the object gained the additional component ${\displaystyle \,v(1-1/n^{2})}$. He supported that hypothesis by supposing that if the density of the external aether was taken as unity, the density of the internal aether was ${\displaystyle n^{2}}$, of which the excess, namely ${\displaystyle \,n^{2}{-}1\,}$, was dragged along at velocity ${\displaystyle v}$, whence the average velocity of the internal aether was ${\displaystyle \,v(1-1/n^{2})}$. The factor in parentheses, which Fresnel originally expressed in terms of wavelengths,^[333] became known as the Fresnel drag coefficient. (See Aether drag hypothesis.)

In his analysis of double refraction, Fresnel supposed that the different refractive indices in different directions within the same medium were due to a directional variation in elasticity, not density (because the concept of mass per unit volume is not directional). But in his treatment of partial reflection, he supposed that the different refractive indices of different media were due to different aether densities, not different elasticities.^[334]

The analogy between light waves and transverse waves in elastic solids does not predict dispersion—that is, the frequency-dependence of the speed of propagation, which enables prisms to produce spectra and causes lenses to suffer from chromatic aberration. Fresnel, in De la Lumière and in the second supplement to his first memoir on double refraction, suggested that dispersion could be accounted for if the particles of the medium exerted forces on each other over distances that were significant fractions of a wavelength.^[335] Later, more than once, Fresnel referred to the demonstration of this result as being contained in a note appended to his "second memoir" on double refraction.^[336] No such note appeared in print, and the relevant manuscripts found after his death showed only that, around 1824, he was comparing refractive indices (measured by Fraunhofer) with a theoretical formula, the meaning of which was not fully explained.^[337]

In the 1830s, Fresnel's suggestion was taken up by Cauchy, Baden Powell, and Philip Kelland, and it was found to be tolerably consistent with the variation of refractive indices with wavelength over the visible spectrum for a variety of transparent media (see Cauchy's equation).^[338] These investigations were enough to show that the wave theory was at least compatible with dispersion; if the model of dispersion was to be accurate over a wider range of frequencies, it needed to be modified so as to take account of resonances within the medium (see Sellmeier equation).^[339]

The analytical complexity of Fresnel's derivation of the ray-velocity surface was an implicit challenge to find a shorter path to the result. This was answered by MacCullagh in 1830, and by William Rowan Hamilton in 1832.^{[340][341][342]}

Within a century of Fresnel's initial stepped-lens proposal, more than 10,000 lights with Fresnel lenses were protecting lives and property around the world.^[344] Concerning the other benefits, the science historian Theresa H. Levitt has remarked:

Everywhere I looked, the story repeated itself. The moment a Fresnel lens appeared at a location was the moment that region became linked into the world economy.^[345]

In the history of physical optics, Fresnel's successful revival of the wave theory nominates him as the pivotal figure between Newton, who held that light consisted of corpuscles, and James Clerk Maxwell, who established that light waves are electromagnetic. Whereas Albert Einstein described Maxwell's work as "the most profound and the most fruitful that physics has experienced since the time of Newton," ^[346] commentators of the era between Fresnel and Maxwell made similarly strong statements about Fresnel:

• MacCullagh, as early as 1830, wrote that Fresnel's mechanical theory of double refraction "would do honour to the sagacity of Newton".^[341]: 78
• Lloyd, in his Report on the progress and present state of physical optics (1834) for the British Association for the Advancement of Science, surveyed previous knowledge of double refraction and declared:

  The theory of Fresnel to which I now proceed,—and which not only embraces all the known phenomena, but has even outstripped observation, and predicted consequences which were afterwards fully verified,—will, I am persuaded, be regarded as the finest generalization in physical science which has been made since the discovery of universal gravitation.^[347]

  In 1841, Lloyd published his Lectures on the Wave-theory of Light, in which he described Fresnel's transverse-wave theory as "the noblest fabric which has ever adorned the domain of physical science, Newton's system of the universe alone excepted." ^[6]
• William Whewell, in all three editions of his History of the Inductive Sciences (1837, 1847, and 1857), at the end of Book IX, compared the histories of physical astronomy and physical optics and concluded:

  It would, perhaps, be too fanciful to attempt to establish a parallelism between the prominent persons who figure in these two histories. If we were to do this, we must consider Huyghens and Hooke as standing in the place of Copernicus, since, like him, they announced the true theory, but left it to a future age to give it development and mechanical confirmation; Malus and Brewster, grouping them together, correspond to Tycho Brahe and Kepler, laborious in accumulating observations, inventive and happy in discovering laws of phenomena; and Young and Fresnel combined, make up the Newton of optical science.^[348]

What Whewell called the "true theory" has since undergone two major revisions. The first, by Maxwell, specified the physical fields whose variations constitute the waves of light. Without the benefit of this knowledge, Fresnel managed to construct the world's first coherent theory of light, showing in retrospect that his methods are applicable to multiple types of waves. The second revision, initiated by Einstein's explanation of the photoelectric effect, supposed that the energy of light waves was divided into quanta, which were eventually identified with particles called photons. But photons did not exactly correspond to Newton's corpuscles; for example, Newton's explanation of ordinary refraction required the corpuscles to travel faster in media of higher refractive index, which photons do not. Neither did photons displace waves; rather, they led to the paradox of wave–particle duality. Moreover, the phenomena studied by Fresnel, which included nearly all the optical phenomena known at his time, are still most easily explained in terms of the wave nature of light. So it was that, as late as 1927, the astronomer Eugène Michel Antoniadi declared Fresnel to be "the dominant figure in optics." ^[349]

• Media related to Augustin Fresnel at Wikimedia Commons

• List of English translations of works by Augustin Fresnel at Zenodo.
• United States Lighthouse Society, especially "Fresnel Lenses Archived 2 March 2021 at the Wayback Machine".
• Works by Augustin-Jean Fresnel at Open Library.
• "Episode 3 – Augustin Fresnel", École polytechnique, 23 January 2019, archived from the original on 22 November 2021 – via YouTube.