This article needs additional citations for verification. (April 2018) |
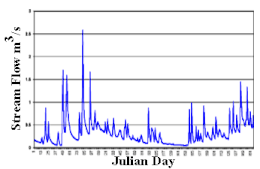
A hydrograph is a graph showing the rate of flow (discharge) versus time past a specific point in a river, channel, or conduit carrying flow. The rate of flow is typically expressed in units of cubic meters per second (m³/s) or cubic feet per second (cfs). Hydrographs often relate changes of precipitation to changes in discharge over time.[1] The term can also refer to a graph showing the volume of water reaching a particular outfall, or location in a sewerage network. Graphs are commonly used in the design of sewerage, more specifically, the design of surface water sewerage systems and combined sewers.
Terminology
[edit]Source:[2]
- Discharge
- the rate of flow (volume per unit time) passing a specific location in a river, or other channel. The discharge is measured at a specific point in a river and is typically time variant.
- Approach Segment
- the river flow before the storm (antecedent flow).
- Rising limb
- The rising limb of the hydrograph, also known as concentration curve, reflects a prolonged increase in discharge from a catchment area, typically in response to a rainfall event.
- Peak discharge
- the highest point on the hydrograph when the rate of discharge is greatest.
- Recession (or falling) limb
- The recession limb extends from the peak flow rate onward. The end of stormflow (a.k.a. quickflow or direct runoff) and the return to groundwater-derived flow (base flow) is often taken as the point of inflection of the recession limb. The recession limb represents the withdrawal of water from the storage built up in the basin during the earlier phases of the hydrograph.
- Lag-1
- autocorrelation method to compare streamflow data to itself by shifting or "lagging" initial discharge dataset 1 time unit. A Lag-10 would mean the initial data is shifted 10 days, then is compared to an unshifted version of the data. Not to be confused with lag time.
- Lag time
- the time interval from the maximum rainfall to the peak discharge.
- Time to peak
- time interval from the start of rainfall to the peak discharge.
- Time of concentration
- Time of concentration is the time from the end of the precipitation period to the end of the quick–response runoff in the hydrograph.[3]
Types of hydrographs include:[4]
- Stream discharge hydrographs
- Stream stage hydrographs
- Precipitation hydrographs
- Storm hydrographs
- Flood hydrographs
- Annual hydrographs a.k.a. regimes
- Direct Runoff Hydrograph
- Effective Runoff Hydrograph
- Raster Hydrograph
- Lag-1 Hydrograph
- Storage opportunities in the drainage network (e.g., lakes, reservoirs, wetlands, channel and bank storage capacity)
Baseflow separation
[edit]A stream hydrograph is commonly determining the influence of different hydrologic processes on discharge from the subject catchment. Because the timing, magnitude, and duration of groundwater return flow differs so greatly from that of direct runoff, separating and understanding the influence of these distinct processes is key to analyzing and simulating the likely hydrologic effects of various land use, water use, weather, and climate conditions and changes.
However, the process of separating “baseflow” from “direct runoff” is an inexact science. In part this is because these two concepts are not, themselves, entirely distinct and unrelated. Return flow from groundwater increases along with overland flow from saturated or impermeable areas during and after a storm event; moreover, a particular water molecule can easily move through both pathways en route to the watershed outlet. Therefore, separation of a purely “baseflow component” in a hydrograph is a somewhat arbitrary exercise. Nevertheless, various graphical and empirical techniques have been developed to perform these hydrograph separations. The separation of base flow from direct runoff can be an important first step in developing rainfall-runoff models for a watershed of interest—for example, in developing and applying unit hydrographs as described below.
Unit hydrograph
[edit]
A unit hydrograph (UH) is the hypothetical unit response of a watershed (in terms of runoff volume and timing) to a unit input of rainfall. It can be defined as the direct runoff hydrograph (DRH) resulting from one unit (e.g., one cm or one inch) of effective rainfall occurring uniformly over that watershed at a uniform rate over a unit period of time. As a UH is applicable only to the direct runoff component of a hydrograph (i.e., surface runoff), a separate determination of the baseflow component is required.
A UH is specific to a particular watershed, and specific to a particular length of time corresponding to the duration of the effective rainfall. That is, the UH is specified as being the 1-hour, 6-hour, or 24-hour UH, or any other length of time up to the time of concentration of direct runoff at the watershed outlet. Thus, for a given watershed, there can be many unit hydrographs, each one corresponding to a different duration of effective rainfall.
The UH technique provides a practical and relatively easy-to-apply tool for quantifying the effect of a unit of rainfall on the corresponding runoff from a particular drainage basin.[5] UH theory assumes that a watershed's runoff response is linear and time-invariant, and that the effective rainfall occurs uniformly over the watershed. In the real world, none of these assumptions are strictly true. Nevertheless, application of UH methods typically yields a reasonable approximation of the flood response of natural watersheds. The linear assumptions underlying UH theory allows for the variation in storm intensity over time (i.e., the storm hyetograph) to be simulated by applying the principles of superposition and proportionality to separate storm components to determine the resulting cumulative hydrograph. This allows for a relatively straightforward calculation of the hydrograph response to any arbitrary rain event.
An instantaneous unit hydrograph is a further refinement of the concept; for an IUH, the input rainfall is assumed to all take place at a discrete point in time (obviously, this isn't the case for actual rainstorms). Making this assumption can greatly simplify the analysis involved in constructing a unit hydrograph, and it is necessary for the creation of a geomorphologic instantaneous unit hydrograph.
The creation of a GIUH is possible given nothing more than topologic data for a particular drainage basin. In fact, only the number of streams of a given order, the mean length of streams of a given order, and the mean land area draining directly to streams of a given order are absolutely required (and can be estimated rather than explicitly calculated if necessary). It is therefore possible to calculate a GIUH for a basin without any data about stream height or flow, which may not always be available.
Subsurface hydrology hydrograph
[edit]In subsurface hydrology (hydrogeology), a hydrograph is a record of the water level (the observed hydraulic head in wells screened across an aquifer).
Typically, a hydrograph is recorded for monitoring of heads in aquifers during non-test conditions (e.g., to observe the seasonal fluctuations in an aquifer). When an aquifer test is being performed, the resulting observations are typically called drawdown, since they are subtracted from pre-test levels and often only the change in water level is dealt with.
Raster hydrograph
[edit]
Raster hydrographs are pixel-based plots for visualizing and identifying variations and changes in large multidimensional data sets. Originally developed by Keim (2000) they were first applied in hydrology by Koehler (2004) as a means of highlighting inter-annual and intra-annual changes in streamflow. The raster hydrographs in WaterWatch, like those developed by Koehler, depict years on the y-axis and days along the x-axis. Users can choose to plot streamflow (actual values or log values), streamflow percentile, or streamflow class (from 1, for low flow, to 7 for high flow), for Daily, 7-Day, 14-Day, and 28-Day streamflow. For a more comprehensive description of raster hydrographs, see Strandhagen et al. (2006).
Lag-1 hydrograph
[edit]A Lag-1 hydrograph is a graph of discharge which can be accomplished without a time axis (Koehler 2022). This technique allows data properties such as Q, dQ/dt, and d2Q/dt2, and trends of increasing, decreasing or no change flow to be readily seen and understood on a single graph. Flow pulse reference lines can easily be added and interpreted. The methodology is based on the time-series serial correlation lag-1 graph and uses the normally unwanted (but still valuable) autocorrelation present within the streamflow data.
The x-axis represents the discharge for a date, Qt, while the y-axis represents the discharge for the next day, Qt+1. Data preparation and plotting methods are identical to an autocorrelation lag 1 plot, where 1 indicates a 1-day or daily time step. The table below shows how the time-series discharge are shifted. It is critical that the temporal sequence is maintained for the data. Thinking of the x values as “flow for today” and the y values as “flow for tomorrow” helps visualize the order of the data.
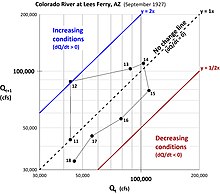
| Date | Qt (x) | Qt+1 (y) |
|---|---|---|
| 11-Sep-1927 | 43,200 | 43,300 |
| 12-Sep-1927 | 43,300 | 88,100 |
| 13-Sep-1927 | 88,100 | 103,000 |
| 14-Sep-1927 | 103,000 | 110,000 |
| 15-Sep-1927 | 110,000 | 78,900 |
| 16-Sep-1927 | 78,900 | 55,900 |
| 17-Sep-1927 | 55,900 | 45,300 |
| 18-Sep-1927 | 45,300 | 33,300 |
See also
[edit]- Aquifer test
- Hydrogeology
- Baseflow
- Routing (hydrology)
- Runoff model (reservoir)
- Stream gauge
- Surface water
References
[edit]- ^ Sherman, LeRoy K. (1932). "The relation of hydrographs of runoff to size and character of drainage-basins". Transactions, American Geophysical Union. 13 (1): 332–339. Bibcode:1932TrAGU..13..332S. doi:10.1029/TR013i001p00332. ISSN 0002-8606.
- ^ "Unit Hydrograph Theory: Terminology and Assumptions". download.comet.ucar.edu. Retrieved 2023-02-28.
- ^ "Unit Hydrograph Theory: Unit Hydrograph Theory Terminology". download.comet.ucar.edu. Retrieved 2023-05-19.
- ^ "Hydrographs - What is a Hydrograph?". geology.com. Retrieved 2023-02-28.
- ^ Holtan, H. N.; Overton, D. E. (1963-01-01). "Analyses and application of simple hydrographs". Journal of Hydrology. 1 (3): 250–264. Bibcode:1963JHyd....1..250H. doi:10.1016/0022-1694(63)90005-2. ISSN 0022-1694.
- Keim, D.A. 2000. Designing pixel-oriented visualization techniques: theory and applications. IEEE Transactions on Visualization and Computer Graphics, 6(1), 59-78.
- Koehler, R. 2004. Raster Based Analysis and Visualization of Hydrologic Time Series. Ph.D. dissertation, University of Arizona. Tucson, AZ, 189 p.
- Koehler, R. 2022. In preparation, The Lag-1 Hydrograph – An Alternate Way to Plot Streamflow Time-Series Data. American Institute of Hydrology Bulletin, Winter 2022.
- Strandhagen, E., Marcus, W.A., and Meacham, J.E. 2006. Views of the rivers: representing streamflow of the greater Yellowstone ecosystem (hotlink to http://geography.uoregon.edu/amarcus/Publications/Strandhagen-et-al_2006_Cart_Pers.pdf). Cartographic Perspectives, no. 55, Fall.
- L. Sherman, "Stream Flow from Rainfall by the Unit Graph Method," Engineering News Record, No. 108, 1932, pp. 501-505.
External links
[edit]- The U.S. Geological Survey (USGS) offers real-time streamflow data for thousands of streams in the United States.
- The U.S. Geological Survey (USGS) also offers an online toolkit to create a raster hydrograph [1] for any of its streamflow gaging stations in the United States.
- SCS Dimensionless Unit Hydrograph.
- SERC activity and Matlab code for calculating and using Unit Hydrograph.