Nucleic acid design is the process of generating a set of nucleic acid base sequences that will associate into a desired conformation. Nucleic acid design is central to the fields of DNA nanotechnology and DNA computing.[2] It is necessary because there are many possible sequences of nucleic acid strands that will fold into a given secondary structure, but many of these sequences will have undesired additional interactions which must be avoided. In addition, there are many tertiary structure considerations which affect the choice of a secondary structure for a given design.[3][4]
Nucleic acid design has similar goals to protein design: in both, the sequence of monomers is rationally designed to favor the desired folded or associated structure and to disfavor alternate structures. However, nucleic acid design has the advantage of being a much computationally simpler problem, since the simplicity of Watson-Crick base pairing rules leads to simple heuristic methods which yield experimentally robust designs. Computational models for protein folding require tertiary structure information whereas nucleic acid design can operate largely on the level of secondary structure. However, nucleic acid structures are less versatile than proteins in their functionality.[2][5]
Nucleic acid design can be considered the inverse of nucleic acid structure prediction. In structure prediction, the structure is determined from a known sequence, while in nucleic acid design, a sequence is generated which will form a desired structure.[2]
Fundamental concepts
[edit]
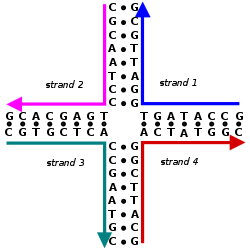
The structure of nucleic acids consists of a sequence of nucleotides. There are four types of nucleotides distinguished by which of the four nucleobases they contain: in DNA these are adenine (A), cytosine (C), guanine (G), and thymine (T). Nucleic acids have the property that two molecules will bind to each other to form a double helix only if the two sequences are complementary, that is, they can form matching sequences of base pairs. Thus, in nucleic acids the sequence determines the pattern of binding and thus the overall structure.[5]
Nucleic acid design is the process by which, given a desired target structure or functionality, sequences are generated for nucleic acid strands which will self-assemble into that target structure. Nucleic acid design encompasses all levels of nucleic acid structure:
- Primary structure—the raw sequence of nucleobases of each of the component nucleic acid strands;
- Secondary structure—the set of interactions between bases, i.e., which parts of which strands are bound to each other; and
- Tertiary structure—the locations of the atoms in three-dimensional space, taking into consideration geometrical and steric constraints.
One of the greatest concerns in nucleic acid design is ensuring that the target structure has the lowest free energy (i.e. is the most thermodynamically favorable) whereas misformed structures have higher values of free energy and are thus unfavored.[2] These goals can be achieved through the use of a number of approaches, including heuristic, thermodynamic, and geometrical ones. Almost all nucleic acid design tasks are aided by computers, and a number of software packages are available for many of these tasks.
Two considerations in nucleic acid design are that desired hybridizations should have melting temperatures in a narrow range, and any spurious interactions should have very low melting temperatures (i.e. they should be very weak).[5] There is also a contrast between affinity-optimizing "positive design", seeks to minimize the energy of the desired structure in an absolute sense, and specificity-optimizing "negative design", which considers the energy of the target structure relative to those of undesired structures. Algorithms which implement both kinds of design tend to perform better than those that consider only one type.[2]
Approaches
[edit]Heuristic methods
[edit]Heuristic methods use simple criteria which can be quickly evaluated to judge the suitability of different sequences for a given secondary structure. They have the advantage of being much less computationally expensive than the energy minimization algorithms needed for thermodynamic or geometrical modeling, and being easier to implement, but at the cost of being less rigorous than these models.
Sequence symmetry minimization is the oldest approach to nucleic acid design and was first used to design immobile versions of branched DNA structures. Sequence symmetry minimization divides the nucleic acid sequence into overlapping subsequences of a fixed length, called the criterion length. Each of the 4N possible subsequences of length N is allowed to appear only once in the sequence. This ensures that no undesired hybridizations can occur which have a length greater than or equal to the criterion length.[2][3]
A related heuristic approach is to consider the "mismatch distance", meaning the number of positions in a certain frame where the bases are not complementary. A greater mismatch distance lessens the chance that a strong spurious interaction can happen.[5] This is related to the concept of Hamming distance in information theory. Another related but more involved approach is to use methods from coding theory to construct nucleic acid sequences with desired properties.
Thermodynamic models
[edit]Information about the secondary structure of a nucleic acid complex along with its sequence can be used to predict the thermodynamic properties of the complex.
When thermodynamic models are used in nucleic acid design, there are usually two considerations: desired hybridizations should have melting temperatures in a narrow range, and any spurious interactions should have very low melting temperatures (i.e. they should be very weak). The Gibbs free energy of a perfectly matched nucleic acid duplex can be predicted using a nearest neighbor model. This model considers only the interactions between a nucleotide and its nearest neighbors on the nucleic acid strand, by summing the free energy of each of the overlapping two-nucleotide subwords of the duplex. This is then corrected for self-complementary monomers and for GC-content. Once the free energy is known, the melting temperature of the duplex can be determined. GC-content alone can also be used to estimate the free energy and melting temperature of a nucleic acid duplex. This is less accurate but also much less computationally costly.[5]
Software for thermodynamic modeling of nucleic acids includes Nupack,[6][7] mfold/UNAFold,[8] and Vienna.[9]
A related approach, inverse secondary structure prediction, uses stochastic local search which improves a nucleic acid sequence by running a structure prediction algorithm and the modifying the sequence to eliminate unwanted features.[5]
Geometrical models
[edit]
Geometrical models of nucleic acids are used to predict tertiary structure. This is important because designed nucleic acid complexes usually contain multiple junction points, which introduces geometric constraints to the system. These constraints stem from the basic structure of nucleic acids, mainly that the double helix formed by nucleic acid duplexes has a fixed helicity of about 10.4 base pairs per turn, and is relatively stiff. Because of these constraints, the nucleic acid complexes are sensitive to the relative orientation of the major and minor grooves at junction points. Geometrical modeling can detect strain stemming from misalignments in the structure, which can then be corrected by the designer.[4][11]
Geometric models of nucleic acids for DNA nanotechnology generally use reduced representations of the nucleic acid, because simulating every atom would be very computationally expensive for such large systems. Models with three pseudo-atoms per base pair, representing the two backbone sugars and the helix axis, have been reported to have a sufficient level of detail to predict experimental results.[11] However, models with five pseudo-atoms per base pair, explicitly including the backbone phosphates, are also used.[12]
Software for geometrical modeling of nucleic acids includes GIDEON,[11] Tiamat,[13] Nanoengineer-1, and UNIQUIMER 3D.[14] Geometrical concerns are especially of interest in the design of DNA origami, because the sequence is predetermined by the choice of scaffold strand. Software specifically for DNA origami design has been made, including caDNAno[15] and SARSE.[16]
Applications
[edit]Nucleic acid design is used in DNA nanotechnology to design strands which will self-assemble into a desired target structure. These include examples such as DNA machines, periodic two- and three-dimensional lattices, polyhedra, and DNA origami.[2] It can also be used to create sets of nucleic acid strands which are "orthogonal", or non-interacting with each other, so as to minimize or eliminate spurious interactions. This is useful in DNA computing, as well as for molecular barcoding applications in chemical biology and biotechnology.[5]
See also
[edit]References
[edit]- ^ Mao, Chengde (December 2004). "The Emergence of Complexity: Lessons from DNA". PLOS Biology. 2 (12): 2036–2038. doi:10.1371/journal.pbio.0020431. ISSN 1544-9173. PMC 535573. PMID 15597116.
- ^ a b c d e f g Dirks, Robert M.; Lin, Milo; Winfree, Erik; Pierce, Niles A. (2004). "Paradigms for computational nucleic acid design". Nucleic Acids Research. 32 (4): 1392–1403. doi:10.1093/nar/gkh291. PMC 390280. PMID 14990744.
- ^ a b Seeman, N (1982). "Nucleic acid junctions and lattices". Journal of Theoretical Biology. 99 (2): 237–47. Bibcode:1982JThBi..99..237S. doi:10.1016/0022-5193(82)90002-9. PMID 6188926.
- ^ a b Sherman, W; Seeman, N (2006). "Design of Minimally Strained Nucleic Acid Nanotubes". Biophysical Journal. 90 (12): 4546–57. Bibcode:2006BpJ....90.4546S. doi:10.1529/biophysj.105.080390. PMC 1471877. PMID 16581842.
- ^ a b c d e f g Brenneman, Arwen; Condon, Anne (2002). "Strand design for biomolecular computation". Theoretical Computer Science. 287: 39–58. doi:10.1016/S0304-3975(02)00135-4.
- ^ Dirks, Robert M.; Bois, Justin S.; Schaeffer, Joseph M.; Winfree, Erik; Pierce, Niles A. (2007). "Thermodynamic Analysis of Interacting Nucleic Acid Strands". SIAM Review. 49 (1): 65–88. Bibcode:2007SIAMR..49...65D. CiteSeerX 10.1.1.523.4764. doi:10.1137/060651100.
- ^ Zadeh, Joseph N.; Wolfe, Brian R.; Pierce, Niles A. (2011). "Nucleic acid sequence design via efficient ensemble defect optimization" (PDF). Journal of Computational Chemistry. 32 (3): 439–452. doi:10.1002/jcc.21633. PMID 20717905. S2CID 1803200.
- ^ Zuker, M. (2003). "Mfold web server for nucleic acid folding and hybridization prediction". Nucleic Acids Research. 31 (13): 3406–15. doi:10.1093/nar/gkg595. PMC 169194. PMID 12824337.
- ^ Gruber AR, Lorenz R, Bernhart SH, Neuböck R, Hofacker IL (2008). "The Vienna RNA websuite". Nucleic Acids Res. 36 (Web Server issue): W70–4. doi:10.1093/nar/gkn188. PMC 2447809. PMID 18424795.
- ^ Goodman, R.P.; Schaap, I.A.T.; Tardin, C.F.; Erben, C.M.; Berry, R.M.; Schmidt, C.F.; Turberfield, A.J. (9 December 2005). "Rapid chiral assembly of rigid DNA building blocks for molecular nanofabrication". Science. 310 (5754): 1661–1665. Bibcode:2005Sci...310.1661G. doi:10.1126/science.1120367. ISSN 0036-8075. PMID 16339440. S2CID 13678773.
- ^ a b c Birac, Jeffrey J.; Sherman, William B.; Kopatsch, Jens; Constantinou, Pamela E.; Seeman, Nadrian C. (2006). "Architecture with GIDEON, a program for design in structural DNA nanotechnology". Journal of Molecular Graphics and Modelling. 25 (4): 470–80. doi:10.1016/j.jmgm.2006.03.005. PMC 3465968. PMID 16630733.
- ^ "PAM3 and PAM5 Model Descriptions". Nanoengineer-1 documentation wiki. Nanorex. Retrieved 2010-04-15.
- ^ Williams, Sean; Lund, Kyle; Lin, Chenxiang; Wonka, Peter; Lindsay, Stuart; Yan, Hao (2009). "Tiamat: A Three-Dimensional Editing Tool for Complex DNA Structures". DNA Computing. Lecture Notes in Computer Science. Vol. 5347. Springer Berlin / Heidelberg. pp. 90–101. doi:10.1007/978-3-642-03076-5_8. ISBN 978-3-642-03075-8. ISSN 0302-9743.
- ^ Zhu, J.; Wei, B.; Yuan, Y.; Mi, Y. (2009). "UNIQUIMER 3D, a software system for structural DNA nanotechnology design, analysis and evaluation". Nucleic Acids Research. 37 (7): 2164–75. doi:10.1093/nar/gkp005. PMC 2673411. PMID 19228709.
- ^ Douglas, S. M.; Marblestone, A. H.; Teerapittayanon, S.; Vazquez, A.; Church, G. M.; Shih, W. M. (2009). "Rapid prototyping of 3D DNA-origami shapes with caDNAno". Nucleic Acids Research. 37 (15): 5001–6. doi:10.1093/nar/gkp436. PMC 2731887. PMID 19531737.
- ^ Andersen, Ebbe S.; Dong, Mingdong; Nielsen, Morten M.; Jahn, Kasper; Lind-Thomsen, Allan; Mamdouh, Wael; Gothelf, Kurt V.; Besenbacher, Flemming; Kjems, JøRgen (2008). "DNA Origami Design of Dolphin-Shaped Structures with Flexible Tails". ACS Nano. 2 (6): 1213–8. doi:10.1021/nn800215j. PMID 19206339.
Further reading
[edit]- Brenneman, Arwen; Condon, Anne (2002). "Strand design for biomolecular computation". Theoretical Computer Science. 287: 39–58. doi:10.1016/S0304-3975(02)00135-4.—A review of approaches to nucleic acid primary structure design.
- Dirks, Robert M.; Lin, Milo; Winfree, Erik; Pierce, Niles A. (2004). "Paradigms for computational nucleic acid design". Nucleic Acids Research. 32 (4): 1392–1403. doi:10.1093/nar/gkh291. PMC 390280. PMID 14990744.—A comparison and evaluation of a number of heuristic and thermodynamic methods for nucleic acid design.
- Seeman, N (1982). "Nucleic acid junctions and lattices". Journal of Theoretical Biology. 99 (2): 237–47. Bibcode:1982JThBi..99..237S. doi:10.1016/0022-5193(82)90002-9. PMID 6188926.—One of the earliest papers on nucleic acid design, describing the use of sequence symmetry minimization to construct immoble branched junctions.
- Andersen, Ebbe Sloth (2010). "Prediction and design of DNA and RNA structures". New Biotechnology. 27 (3): 184–193. doi:10.1016/j.nbt.2010.02.012. PMID 20193785.—A review comparing the capabilities of available nucleic acid design software.