| Tridiminished icosahedron | |
|---|---|
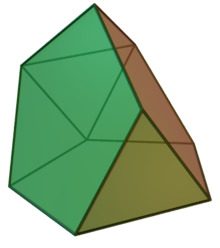 | |
| Type | Johnson J62 – J63 – J64 |
| Faces | 5 triangles 3 pentagons |
| Edges | 15 |
| Vertices | 9 |
| Vertex configuration | |
| Symmetry group | |
| Properties | convex, non-composite |
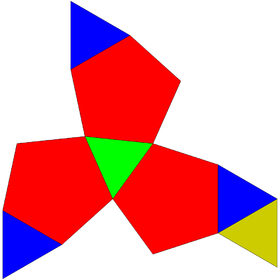
| Net | |
 | |
In geometry, the tridiminished icosahedron is a Johnson solid that is constructed by removing three pentagonal pyramids from a regular icosahedron.
Construction
[edit]The tridiminished icosahedron can be constructed by removing three regular pentagonal pyramid from a regular icosahedron.[1] The aftereffect of such construction leaves five equilateral triangles and three regular pentagons.[2] Since all of its faces are regular polygons and the resulting polyhedron remains convex, the tridiminished icosahedron is a Johnson solid, and it is enumerated as the sixty-third Johnson solid .[3] This construction is similar to other Johnson solids as in gyroelongated pentagonal pyramid and metabidiminished icosahedron.[1]
The tridiminished icosahedron is non-composite polyhedron, meaning it is convex polyhedron that cannot be separated by a plane into two or more regular polyhedrons.[4]
Properties
[edit]The surface area of a tridiminished icosahedron is the sum of all polygonal faces' area: five equilateral triangles and three regular pentagons. Its volume can be ascertained by subtracting the volume of a regular icosahedron with the volume of three pentagonal pyramids. Given that is the edge length of a tridiminished icosahedron, they are:[2]
See also
[edit]- Snub 24-cell, a 4-polytope whose vertex figure is a tridiminished icosahedron
References
[edit]- ^ a b Gailiunas, Paul (2001), "A Polyhedral Byway" (PDF), in Sarhangi, Reza; Jablan, Slavik (eds.), Bridges: Mathematical Connections in Art, Music, and Science, Bridges Conference, pp. 115–122.
- ^ a b Berman, Martin (1971), "Regular-faced convex polyhedra", Journal of the Franklin Institute, 291 (5): 329–352, doi:10.1016/0016-0032(71)90071-8, MR 0290245.
- ^ Francis, Darryl (August 2013), "Johnson solids & their acronyms", Word Ways, 46 (3): 177
- ^ Timofeenko, A. V. (2009), "Convex Polyhedra with Parquet Faces" (PDF), Docklady Mathematics, 80 (2): 720–723, doi:10.1134/S1064562409050238.






